题目内容
30、在△ABC内有一点P1,当P1、A、B、C没有任何三点在同一直线上时,则可构成3个互不重叠的小三角形(如图①).
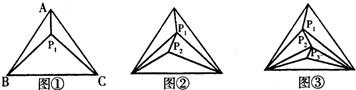
当三角形内有两个点P1、P2时,如图②,其它条件不变,可构成的互不重叠的小三角形的个数是多少?答:
当三角形内有三个点P1、P2、P3时,如图③,其它条件不变,可构成的互不重叠的小三角形的个数是多少?答:
一般地,当三角形内有n(n为正整数)个点时,其它条件不变,可构成的互不重叠的小三角形的个数是多少?答:
特别,当三角形内有2006个点时,其它条件不变,可构成多少个互不重叠的小三角形.答

当三角形内有两个点P1、P2时,如图②,其它条件不变,可构成的互不重叠的小三角形的个数是多少?答:
5个
;当三角形内有三个点P1、P2、P3时,如图③,其它条件不变,可构成的互不重叠的小三角形的个数是多少?答:
7个
;一般地,当三角形内有n(n为正整数)个点时,其它条件不变,可构成的互不重叠的小三角形的个数是多少?答:
(2n+1)个
;特别,当三角形内有2006个点时,其它条件不变,可构成多少个互不重叠的小三角形.答
4013个
.分析:三角形中有一个点时,三角形的个数为2×1+1=3个;
三角形中有2个点时,三角形的个数为2×2+1=5个;
…
依规律得到三角形内有n(n为正整数)个点时,三角形的个数;
把n=2006代入计算即可.
三角形中有2个点时,三角形的个数为2×2+1=5个;
…
依规律得到三角形内有n(n为正整数)个点时,三角形的个数;
把n=2006代入计算即可.
解答:解:三角形中有一个点时,三角形的个数为2×1+1=3个;
三角形中有2个点时,三角形的个数为2×2+1=5个;
三角形中有3个点时,三角形的个数为2×3+1=7个;
三角形中有n个点时,三角形的个数为(2n+1)个;
∴当三角形内有2006个点时,三角形的个数为2×2006+1=4013个;
故答案为5个,7个,(2n+1)个,4013个.
三角形中有2个点时,三角形的个数为2×2+1=5个;
三角形中有3个点时,三角形的个数为2×3+1=7个;
三角形中有n个点时,三角形的个数为(2n+1)个;
∴当三角形内有2006个点时,三角形的个数为2×2006+1=4013个;
故答案为5个,7个,(2n+1)个,4013个.
点评:考查图形的规律性变化;得到三角形的个数与三角形内点的个数的变化规律是解决本题的关键.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
 21、(1)如图,在∠ABC内有一点O,
21、(1)如图,在∠ABC内有一点O,
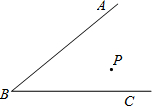 如图,在∠ABC内有一点P,问:
如图,在∠ABC内有一点P,问: