Question

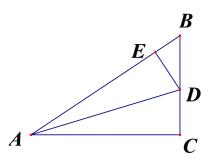
【题目】已知：如图，Rt△ABC中，∠C=90°，AC=8，BC=6，AD平分∠BAC，交BC于点D，DE⊥AB于点E.

（1）求BE的长；

（2）求BD的长.

Answer 1

【答案】（1）2 （2）

【解析】(1)、根据勾股定理求出AB的长度，然后根据角平分线得出△EAD和△CAD全等，从而得出AE=AC=8，最后求出BE的长度；(2)、折DC=x，则DE=x，BD=6－x，然后根据Rt△BDE的勾股定理求出x的值，从而得出BD的长度．

(1)、在Rt△ABC中， ∵AC=8，BC=6， ∴AB=10， ∵AD平分∠BAC，∴∠EAD=∠CAD，

∴△EAD≌△CAD（AAS）， ∴AE=AC=8， ∴BE=10-8=2；

(2)、∵△EAD≌△CAD， ∴ED=DC， 设DC=x,则ED=x. ∵BC=6，∴BD=6-x，

在Rt△BED中，根据勾股定理得： 解得x=，∴BD=6-=．