题目内容
已知抛物线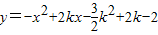 (k是实数)与x轴有交点,将此抛物线向左平移1个单位,再向上平移4个单位,得到新的抛物线E,设抛物线E与x轴的交点为B,C,如图.
(k是实数)与x轴有交点,将此抛物线向左平移1个单位,再向上平移4个单位,得到新的抛物线E,设抛物线E与x轴的交点为B,C,如图.(1)求抛物线E所对应的函数关系式,并求出顶点A的坐标;
(2)连接AB,把AB所在的直线平移,使它经过点C,得到直线l,点P是l上一动点(与点C不重合).设以点A,B,C,P为顶点的四边形面积为S,点P的横坐标为t,当0<S≤16时,求t的取值范围;
(3)点Q是直线l上的另一个动点,以点Q为圆心,R为半径作圆Q,当R取何值时,圆Q与直线AB相切?相交?相离?直接给出结果.

【答案】分析:(1)首先根据抛物线与x轴有交点,则判别式△≥0,据此即可求得k的值,函数的解析式即可求得,然后根据将此抛物线向左平移1个单位,再向上平移4个单位,得到新的抛物线E,即可求得E的解析式以及顶点坐标;
(2)首先求得B、C的坐标,然后利用待定系数法即可求得AB,l的解析式,分P在x轴下方和上方,两种情况利用P的横坐标t表示出四边形的面积,再根据0<S≤16即可得到关于t的不等式,求得t的范围;
(3)过点C作CH⊥AB,H为垂足,利用三角形的面积公式求得CH的长,然后利用直线与圆的位置关系的判定方法,即可写出结果.
解答:解:(1)抛物线y=-x2+2kx- k2+2k-2(k是实数)与x轴有交点,
k2+2k-2(k是实数)与x轴有交点,
则判别式△=(2k)2+4(- k2+2k-2)=-(k-2)2≥0,
k2+2k-2)=-(k-2)2≥0,
则k=2,
因而抛物线的解析式是:y=-x2+4x-4,
将此抛物线向左平移1个单位,再向上平移4个单位得到的抛物线是:y=-(x+1)2+4(x+1)-4+4,
即:y=-x2+2x+3
即y=-(x-1)2+4,
∴顶点A坐标为(1,4);
(2)令y=0,得-x2+2x+3=0所以B(-1,0),C(3,0)
设直线AB的函数关系式为y=kx+b、
∵A(0,4),B(-1,0)∴ 解得
解得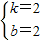 ,
,
∴y=2x+2
∵直线l∥AB且过点C(3,0),∴直线l的函数关系式为y=2x-6,
∵点P是l上一动点且横坐标为t,∴点P坐标为(t,2t-6)
当P在x轴下方时(t<3),S=S△ABC+S△BCP= ×4×4+
×4×4+ ×4×|2t-6|=20-4t.
×4×|2t-6|=20-4t.
∵0<S≤16,∴0<20-4t≤16,∴1≤t<5、又t<3,∴1≤t<3
当P在x轴上方时(t>3),
作PM⊥x轴于M,设对称轴与x轴交点为N. 则
S=S梯形ANMP+S△ANB+S△PMC
= [4+(2t-6)]•(t-1)+
[4+(2t-6)]•(t-1)+ 2×4-
2×4- (t-3)(2t-6)
(t-3)(2t-6)
=4t-4
另法:∵直线l∥AB,根据等底等高的面积相等进行转化
S=S△ABC+S△APC=S△ABC+S△BPC=S△ABC+S△PBC= ×4×4+
×4×4+ ×4×(2t-6)=4t-4
×4×(2t-6)=4t-4
∵0<S≤16,∴0<4t-4≤16,
∴1<t≤5.
又∵t>3,
∴3<t≤5.
∴t的取值范围是1≤t<3或3<t≤5;
(3)AB=2 ,过点C作CH⊥AB,H为垂足,S△ABC=
,过点C作CH⊥AB,H为垂足,S△ABC= ×4×4=
×4×4= ×AB×CH
×AB×CH
所以CH= ,
,
因为平行线间距离处处相等,所以点Q到直线AB的距离等于 ,
,
所以当R= 时相切,R
时相切,R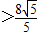 时相交,R<
时相交,R< 时相离.
时相离.
点评:此题考查了待定系数法求抛物线解析式以及直线与圆的位置关系的判定,并且用到了分类讨论的数学思想,难点在于考虑问题要全面,做到不重不漏.
(2)首先求得B、C的坐标,然后利用待定系数法即可求得AB,l的解析式,分P在x轴下方和上方,两种情况利用P的横坐标t表示出四边形的面积,再根据0<S≤16即可得到关于t的不等式,求得t的范围;
(3)过点C作CH⊥AB,H为垂足,利用三角形的面积公式求得CH的长,然后利用直线与圆的位置关系的判定方法,即可写出结果.
解答:解:(1)抛物线y=-x2+2kx-
 k2+2k-2(k是实数)与x轴有交点,
k2+2k-2(k是实数)与x轴有交点,则判别式△=(2k)2+4(-
 k2+2k-2)=-(k-2)2≥0,
k2+2k-2)=-(k-2)2≥0,则k=2,
因而抛物线的解析式是:y=-x2+4x-4,

将此抛物线向左平移1个单位,再向上平移4个单位得到的抛物线是:y=-(x+1)2+4(x+1)-4+4,
即:y=-x2+2x+3
即y=-(x-1)2+4,
∴顶点A坐标为(1,4);
(2)令y=0,得-x2+2x+3=0所以B(-1,0),C(3,0)
设直线AB的函数关系式为y=kx+b、
∵A(0,4),B(-1,0)∴
 解得
解得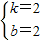 ,
,∴y=2x+2
∵直线l∥AB且过点C(3,0),∴直线l的函数关系式为y=2x-6,
∵点P是l上一动点且横坐标为t,∴点P坐标为(t,2t-6)

当P在x轴下方时(t<3),S=S△ABC+S△BCP=
 ×4×4+
×4×4+ ×4×|2t-6|=20-4t.
×4×|2t-6|=20-4t.∵0<S≤16,∴0<20-4t≤16,∴1≤t<5、又t<3,∴1≤t<3
当P在x轴上方时(t>3),
作PM⊥x轴于M,设对称轴与x轴交点为N. 则
S=S梯形ANMP+S△ANB+S△PMC
=
 [4+(2t-6)]•(t-1)+
[4+(2t-6)]•(t-1)+ 2×4-
2×4- (t-3)(2t-6)
(t-3)(2t-6)=4t-4
另法:∵直线l∥AB,根据等底等高的面积相等进行转化
S=S△ABC+S△APC=S△ABC+S△BPC=S△ABC+S△PBC=
 ×4×4+
×4×4+ ×4×(2t-6)=4t-4
×4×(2t-6)=4t-4∵0<S≤16,∴0<4t-4≤16,
∴1<t≤5.
又∵t>3,
∴3<t≤5.
∴t的取值范围是1≤t<3或3<t≤5;
(3)AB=2
 ,过点C作CH⊥AB,H为垂足,S△ABC=
,过点C作CH⊥AB,H为垂足,S△ABC= ×4×4=
×4×4= ×AB×CH
×AB×CH所以CH=
 ,
,因为平行线间距离处处相等,所以点Q到直线AB的距离等于
 ,
,所以当R=
 时相切,R
时相切,R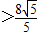 时相交,R<
时相交,R< 时相离.
时相离.点评:此题考查了待定系数法求抛物线解析式以及直线与圆的位置关系的判定,并且用到了分类讨论的数学思想,难点在于考虑问题要全面,做到不重不漏.

练习册系列答案
相关题目
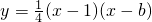 (b是实数且b>2)与x轴的正半轴分别交于点A、B(点A位于点B的左侧),与y轴的正半轴交于点C.
(b是实数且b>2)与x轴的正半轴分别交于点A、B(点A位于点B的左侧),与y轴的正半轴交于点C.
 (b是实数且b>2)与x轴的正半轴分别交于点A、B(点A位于点B的左侧),与y轴的正半轴交于点C.
(b是实数且b>2)与x轴的正半轴分别交于点A、B(点A位于点B的左侧),与y轴的正半轴交于点C.
 (k是实数)与x轴有交点,将此抛物线向左平移1个单位,再向上平移4个单位,得到新的抛物线E,设抛物线E与x轴的交点为B,C,如图.
(k是实数)与x轴有交点,将此抛物线向左平移1个单位,再向上平移4个单位,得到新的抛物线E,设抛物线E与x轴的交点为B,C,如图.
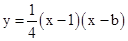 (b是实数且b>2)与x轴的正半轴分别交于点A、B(点A位于点B的左侧),与y轴的正半轴交于点C.
(b是实数且b>2)与x轴的正半轴分别交于点A、B(点A位于点B的左侧),与y轴的正半轴交于点C.