题目内容
问题背景:
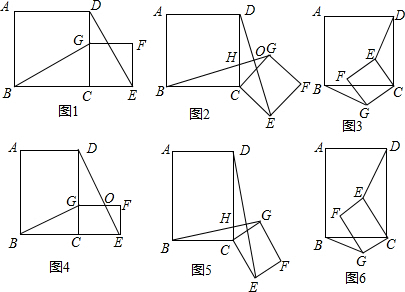
如图1,矩形铁片ABCD的长为2a,宽为a; 为了要让铁片能穿过直径为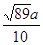 的圆孔,需对铁片进行处理(规定铁片与圆孔有接触时铁片不能穿过圆孔);
的圆孔,需对铁片进行处理(规定铁片与圆孔有接触时铁片不能穿过圆孔);
探究发现:
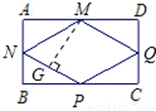
1.如图2,M、N、P、Q分别是AD、AB、BC、CD的中点,若将矩形铁片的四个角去掉,只余下四边形MNPQ,则此时铁片的形状是 _______,给出证明,并通过计算说明此时铁片都能穿过圆孔;
拓展迁移:
2.如图3,过矩形铁片ABCD的中心作一条直线分别交边BC、AD于点E、F(不与端点重合),沿着这条直线将矩形 铁片切割成两个全等的直角梯形铁片;
①当BE=DF=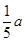 时,判断直角梯形铁片EBAF能否穿过圆孔,并说明理由;
时,判断直角梯形铁片EBAF能否穿过圆孔,并说明理由;
②为了能使直角梯形铁片EBAF顺利穿过圆孔,请直接写出线段BE的长度的取值范围 .
1.是菱形
如图,过点M作MG⊥NP于点G,∵M、N、P、Q分别是AD、AB、BC、
CD的中点,∴△AMN≌△BPN≌△CPQ≌△DMQ,∴MN=NP=PQ=QM,
∴四边形MNPQ是菱形,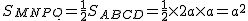 ,MN=
,MN= ,∴MG=
,∴MG= ,∴此时铁片能穿过圆。
,∴此时铁片能穿过圆。
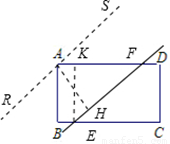
2.①如图,过点A作AH⊥EF于点H,过点E作EK⊥AD于点K
显然AB=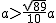 ,
故沿着与AB垂直的方向无法穿过圆孔
,
故沿着与AB垂直的方向无法穿过圆孔
过点A作EF的平行线RS,故只需计算直线RS与EF之间的距离即可
∵BE=AK=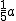 ,EK=AB=a,AF=
,EK=AB=a,AF=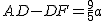
∴KF=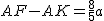 ,EF=
,EF= ,∵∠AHF=∠EKF=90°,∠AFH=∠EFK
,∵∠AHF=∠EKF=90°,∠AFH=∠EFK
∴△AHF∽△EKF ∴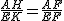 ,可得AH=
,可得AH= ,
,
∴该直角梯形铁片不能穿过圆孔
②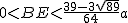 或
或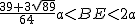 .…
.…
【解析】
1.利用四条边相等的四边形为矩形来判定四边形为菱形,然后利用面积相等来求得菱形一边的高,与已知数据比较后判断是否能通过.
2.利用两三角形相似得到比例线段,进而求出点A到EF的距离,然后与已知线段比较,从而判定能否通过.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案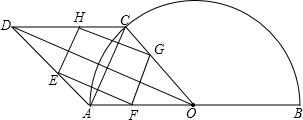 值,判断此时四边形EFGH的形状,并说明理由.
值,判断此时四边形EFGH的形状,并说明理由. (2011•临川区模拟)问题背景:如图1,四边形ABCD和CEFG都是正方形,B,C,E在同一条直线上,连接BG,DE.
(2011•临川区模拟)问题背景:如图1,四边形ABCD和CEFG都是正方形,B,C,E在同一条直线上,连接BG,DE.
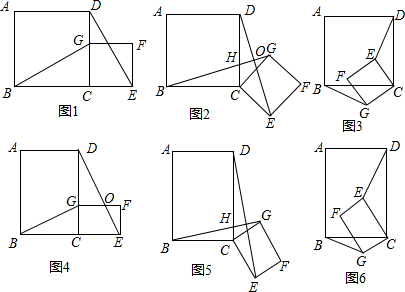 问题背景:如图1,四边形ABCD和CEFG都是正方形,B,C,E在同一条直线上,连接BG,DE.
问题背景:如图1,四边形ABCD和CEFG都是正方形,B,C,E在同一条直线上,连接BG,DE.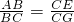 =k(其中k>0),请直接写出线段BG、DE的数量关系及位置关系.请选择图5或图6证明你的判断.
=k(其中k>0),请直接写出线段BG、DE的数量关系及位置关系.请选择图5或图6证明你的判断.