题目内容
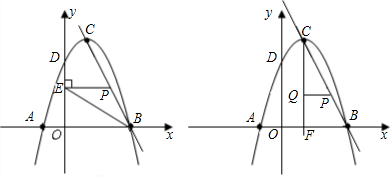
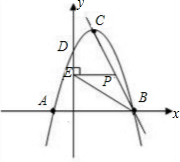 如图,在直角坐标系中,抛物线y=-x2+2x+c与y轴交于点D(0,3).
如图,在直角坐标系中,抛物线y=-x2+2x+c与y轴交于点D(0,3).
(1)直接写出c的值;
(2)若抛物线与x轴交于A、B两点(点B在点A的右边),顶点为C点,求直线BC的解析式;
(3)已知点P是直线BC上一个动点,
①当点P在线段BC上运动时(点P不与B、C重合),过点P作PE⊥y轴,垂足为E,连接BE.设点P的坐标为(x,y),△PBE的面积为s,求s与x的函数关系式,写出自变量x的取值范围,并求出s的最大值;
②试探索:在直线BC上是否存在着点P,使得以点P为圆心,半径为r的⊙P,既与抛物线的对称轴相切,又与以点C为圆心,半径为1的⊙C相切?如果存在,试求r的值,并直接写出点P的坐标;如果不存在,请说明理由.
解:(1)c=3.
(2)由(1)知抛物线为:y=-x2+2x+3,配方得y=-(x-1)2+4
∴顶点C坐标为(1,4)
令y=0得x1=-1,x2=3,
∴B(3,0)
设直线BC解析式为:y=kx+b(k≠0),把B、C两点坐标代入,
得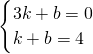 ,
,
解得:k=-2,b=6,
∴直线BC解析式为:y=-2x+6,
(3)①∵点P(x,y)在y=-2x+6的图象上,
∴PE=x,OE=-2x+6
∴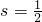 PE•OE=
PE•OE=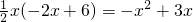
∴s=-x2+3x (1<x<3),
s=-(x2-3x+ )+
)+ =-(x-
=-(x- )2+
)2+ .
.
∵ 符合1<x<3,
符合1<x<3,
∴当 时,s取得最大值,最大值为
时,s取得最大值,最大值为 .
.
②答:存在.
如图,设抛物线的对称轴交x轴于点F,则CF=4,BF=2.
过P作PQ⊥CF于Q,则Rt△CPQ∽Rt△CBF
∴ ,
,
∴CQ=2r,
当⊙P与⊙C外切时,CP=r+1.
∵CQ2+PQ2=CP2,
∴(2r)2+r2=(r+1)2
解得 舍去).
舍去).
此时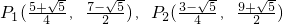 .
.
当⊙P与⊙C内切时,CP=r-1.
∵CQ2+PQ2=CP2,
∴(2r)2+r2=(r-1)2.
解得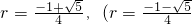 舍去).
舍去).
此时 .
.
∴当⊙P与⊙C相切时.
点P的坐标为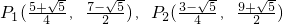 ,
, .
.
(点P的坐标只写1个不得分,写出2个或3个得,写出4个得2分)
分析:(1)将D(0,3),直接代入解析式求出即可;
(2)分别求出顶点C坐标为(1,4)以及令y=0得x1=-1,x2=3得出B(3,0),代入一次函数解析式即可得出直线BC的解析式;
(3)根据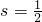 PE•OE=
PE•OE=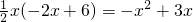 ,求出s最大值即可,再根据当⊙P与⊙C外切时,以及当⊙P与⊙C内切时,分别得出P点的坐标.
,求出s最大值即可,再根据当⊙P与⊙C外切时,以及当⊙P与⊙C内切时,分别得出P点的坐标.
点评:此题主要考查了二次函数的综合应用以及直线解析式的求法,根据圆与圆的相切时分类讨论,考查学生分类讨论,数形结合的数学思想方法.
(2)由(1)知抛物线为:y=-x2+2x+3,配方得y=-(x-1)2+4
∴顶点C坐标为(1,4)
令y=0得x1=-1,x2=3,
∴B(3,0)
设直线BC解析式为:y=kx+b(k≠0),把B、C两点坐标代入,
得
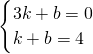 ,
,解得:k=-2,b=6,
∴直线BC解析式为:y=-2x+6,
(3)①∵点P(x,y)在y=-2x+6的图象上,
∴PE=x,OE=-2x+6
∴
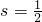 PE•OE=
PE•OE=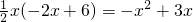
∴s=-x2+3x (1<x<3),
s=-(x2-3x+
 )+
)+ =-(x-
=-(x- )2+
)2+ .
.∵
 符合1<x<3,
符合1<x<3,∴当
 时,s取得最大值,最大值为
时,s取得最大值,最大值为 .
.
②答:存在.
如图,设抛物线的对称轴交x轴于点F,则CF=4,BF=2.
过P作PQ⊥CF于Q,则Rt△CPQ∽Rt△CBF
∴
 ,
,∴CQ=2r,
当⊙P与⊙C外切时,CP=r+1.
∵CQ2+PQ2=CP2,
∴(2r)2+r2=(r+1)2
解得
 舍去).
舍去).此时
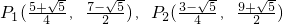 .
.当⊙P与⊙C内切时,CP=r-1.
∵CQ2+PQ2=CP2,
∴(2r)2+r2=(r-1)2.
解得
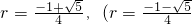 舍去).
舍去).此时
 .
.∴当⊙P与⊙C相切时.
点P的坐标为
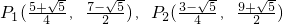 ,
, .
.(点P的坐标只写1个不得分,写出2个或3个得,写出4个得2分)
分析:(1)将D(0,3),直接代入解析式求出即可;
(2)分别求出顶点C坐标为(1,4)以及令y=0得x1=-1,x2=3得出B(3,0),代入一次函数解析式即可得出直线BC的解析式;
(3)根据
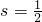 PE•OE=
PE•OE=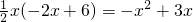 ,求出s最大值即可,再根据当⊙P与⊙C外切时,以及当⊙P与⊙C内切时,分别得出P点的坐标.
,求出s最大值即可,再根据当⊙P与⊙C外切时,以及当⊙P与⊙C内切时,分别得出P点的坐标.点评:此题主要考查了二次函数的综合应用以及直线解析式的求法,根据圆与圆的相切时分类讨论,考查学生分类讨论,数形结合的数学思想方法.

练习册系列答案
相关题目

 如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.
如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.

 ,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件:
,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件: