题目内容
 如图,已知反比例函数
如图,已知反比例函数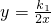 的图象与一次函数y=k2x+b的图象交于A,B两点,A(1,n),B(-
的图象与一次函数y=k2x+b的图象交于A,B两点,A(1,n),B(- ,-2).
,-2).
(1)求反比例函数和一次函数的解析式;
(2)在x轴上是否存在点P,使△AOP为等腰三角形?若存在,请你直接写出P点的坐标;若不存在,请说明理由.
解:(1)∵点B(- ,-2)在反比例函数
,-2)在反比例函数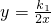 图象上,
图象上,
∴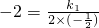
∴k1=2
∴反比例函数的解析式为 ,
,
又∵A(1,n)在反比例函数图象上,
∴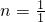 ,
,
∴n=1;
∴A点坐标为(1,1);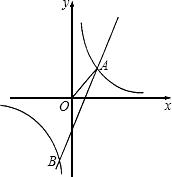
∴一次函数y=k2x+b的图象经过点A(1,1),B(- ,-2);
,-2);
∴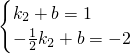 ,∴
,∴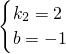 ;
;
∴一次函数的解析式为y=2x-1;
(2)存在符合条件的点P.
若OA=OP,则P( ,0)或(-
,0)或(- ,0),
,0),
若AP=OA,则P(2,0),
若OP=AP,则(1,0),
可求出点P的坐标为( ,0),(-
,0),(- ,0),(2,0),(1,0).
,0),(2,0),(1,0).
分析:(1)把点B(- ,-2)坐标代入反比例函数
,-2)坐标代入反比例函数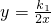 ,求出反比例函数解析式.再求出A(1,n)的坐标,根据A、B的坐标,即可求得一次函数的解析式;
,求出反比例函数解析式.再求出A(1,n)的坐标,根据A、B的坐标,即可求得一次函数的解析式;
(2)以O为圆心,OA为半径,交x轴于两点,这两点均符合点P的要求.以A为圆心,AO为半径,交x轴于一点,作AO的垂直平分线,交x轴于一点,因此共有4个符合要求的点.
点评:本题考查反比例函数和一次函数解析式的确定、等腰三角形的判定等知识及综合应用知识、解决问题的能力.要注意(2)在不确定等腰三角形的腰和底的情况下要考虑到所有的情况,不要漏解.
 ,-2)在反比例函数
,-2)在反比例函数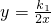 图象上,
图象上,∴
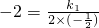
∴k1=2
∴反比例函数的解析式为
 ,
,又∵A(1,n)在反比例函数图象上,
∴
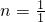 ,
,∴n=1;
∴A点坐标为(1,1);

∴一次函数y=k2x+b的图象经过点A(1,1),B(-
 ,-2);
,-2);∴
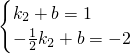 ,∴
,∴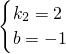 ;
;∴一次函数的解析式为y=2x-1;
(2)存在符合条件的点P.
若OA=OP,则P(
 ,0)或(-
,0)或(- ,0),
,0),若AP=OA,则P(2,0),
若OP=AP,则(1,0),
可求出点P的坐标为(
 ,0),(-
,0),(- ,0),(2,0),(1,0).
,0),(2,0),(1,0).分析:(1)把点B(-
 ,-2)坐标代入反比例函数
,-2)坐标代入反比例函数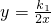 ,求出反比例函数解析式.再求出A(1,n)的坐标,根据A、B的坐标,即可求得一次函数的解析式;
,求出反比例函数解析式.再求出A(1,n)的坐标,根据A、B的坐标,即可求得一次函数的解析式;(2)以O为圆心,OA为半径,交x轴于两点,这两点均符合点P的要求.以A为圆心,AO为半径,交x轴于一点,作AO的垂直平分线,交x轴于一点,因此共有4个符合要求的点.
点评:本题考查反比例函数和一次函数解析式的确定、等腰三角形的判定等知识及综合应用知识、解决问题的能力.要注意(2)在不确定等腰三角形的腰和底的情况下要考虑到所有的情况,不要漏解.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
 如图,已知反比例函数
如图,已知反比例函数 如图,已知反比例函数
如图,已知反比例函数 如图,已知反比例函数y=
如图,已知反比例函数y= 如图,已知反比例函数
如图,已知反比例函数 如图,已知反比例函数y=
如图,已知反比例函数y=