��Ŀ����
�Ķ�����һ�λ��������������⣮�۲�����һ������1��2��4��8���������Ƿ��֣���һ�����ӵڶ�����ÿһ������ǰһ��ıȶ�����2��
һ��أ����һ�����ӵڶ�����ÿһ������ǰһ��ıȶ�����ͬһ����������һ�����ͽ����ȱ����У�������������ȱ����еıȣ�
��1���ȱ�����5��-15��45�����ĵ�������
��2�����һ����a1��a2��a3��a4�����ǵȱ����У��ҹ���Ϊq����ô���������Ĺ涨����
| a2 |
| a1 |
| a3 |
| a2 |
| a4 |
| a3 |
��3��һ���ȱ����еĵڶ�����10����������20�������ĵ�һ����
��������1������-15��5=-3��45�£�-15��=-3�����Կ��Ը��ݹ��ɵõ������
��2��ͨ���۲췢�֣���n��������a1���Թ���q�ģ�n-1���η��������Ϳ����Ƴ���ʽ�ˣ�
��3�����ڵڶ�����10����������20���ɴ˿��Եõ����ȣ�Ȼ��Ϳ��Եõ���һ��͵����
��2��ͨ���۲췢�֣���n��������a1���Թ���q�ģ�n-1���η��������Ϳ����Ƴ���ʽ�ˣ�
��3�����ڵڶ�����10����������20���ɴ˿��Եõ����ȣ�Ȼ��Ϳ��Եõ���һ��͵����
����⣺��1����-15��5=-3��45�£�-15��=-3��
�������Ϊ45����-3��=-135��
����մ𰸣�-135��
��2��ͨ���۲췢�֣���n��������a1���Թ���q�ģ�n-1���η�������an=a1qn-1��
����մ𰸣�a1qn-1��
��3���߹��ȵ���20��10=2��
���һ����ڣ�10��2=5��
���������20��2=40��an=a1qn-1��
����մ𰸣����ĵ�һ����5����������40��
�������Ϊ45����-3��=-135��
����մ𰸣�-135��
��2��ͨ���۲췢�֣���n��������a1���Թ���q�ģ�n-1���η�������an=a1qn-1��
����մ𰸣�a1qn-1��
��3���߹��ȵ���20��10=2��
���һ����ڣ�10��2=5��
���������20��2=40��an=a1qn-1��
����մ𰸣����ĵ�һ����5����������40��
�������������Ķ������⣬������ʽ�ij�����������Ŀ��Ϣ�ǽ���Ĺؼ�������һ�����ǰһ����ڹ��ȣ���n��������a1���Թ���q�ģ�n-1���η���

��ϰ��ϵ�д�
�����Ŀ
 ��
�� ��
�� ��
�� �������ǵȱ����У��ҹ���Ϊq����ô���������涨����
�������ǵȱ����У��ҹ���Ϊq����ô���������涨����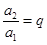 ��
��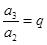 ��
��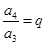 ����������
����������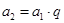 ��
��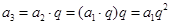 ��
��
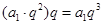 ��������
��������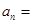 ����
����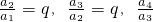 =��������a2=a1q��a3=a2q=��a1q��q=a1q2��a4=a3q=��a1q2��q=a1q3������an=______���ú�a1��q�Ĵ���ʽ��ʾ����
=��������a2=a1q��a3=a2q=��a1q��q=a1q2��a4=a3q=��a1q2��q=a1q3������an=______���ú�a1��q�Ĵ���ʽ��ʾ����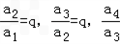 =��������a2=a1q��a3=a2q=��a1q��q=a1q2��a4=a3q=��a1q2��q=a1q3������an= ���ú�a1��q�Ĵ���ʽ��ʾ����
=��������a2=a1q��a3=a2q=��a1q��q=a1q2��a4=a3q=��a1q2��q=a1q3������an= ���ú�a1��q�Ĵ���ʽ��ʾ����