题目内容
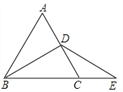
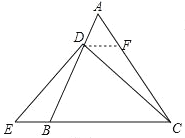
【题目】(1)已知△ABC是等腰三角形,其底边是BC,点D在线段AB上,E是直线BC上一点,且∠DEC=∠DCE,若∠A等于60°(如图①).求证:EB=AD;
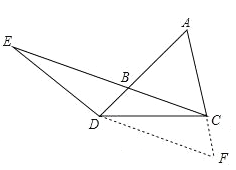
(2)若将(1)中的“点D在线段AB上”改为“点D在线段AB的延长线上”,其他条件不变(如图②),(1)的结论是否成立,并说明理由。
【答案】(1)证明见解析(2)证明见解析
【解析】试题分析:(1)作DF∥BC交AC于F,由平行线的性质得出∠ADF=∠ABC,∠AFD=∠ACB,∠FDC=∠DCE,证明△ABC是等边三角形,得出∠ABC=∠ACB=60°,证出△ADF是等边三角形,∠DFC=120°,得出AD=DF,由已知条件得出∠FDC=∠DEC,ED=CD,由AAS证明△DBE≌△CFD,得出EB=DF,即可得出结论;
(2)作DF∥BC交AC的延长线于F,同(1)证出△DBE≌△CFD,得出EB=DF,即可得出结论.
试题解析:(1)证明:如图,作DF∥BC交AC于F,
则△ADF为等边三角形
∴AD=DF,又∵ ∠DEC=∠DCB,
∠DEC+∠EDB=60°,
∠DCB+∠DCF=60° ,
∴ ∠EDB=∠DCA ,DE=CD,
在△DEB和△CDF中,
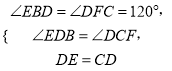
∴△DEB≌△CDF,
∴BD=DF,
∴BE=AD .
(2). EB=AD成立;
理由如下:作DF∥BC交AC的延长线于F,如图所示:
同(1)得:AD=DF,∠FDC=∠ECD,∠FDC=∠DEC,ED=CD,
又∵∠DBE=∠DFC=60°,
∴△DBE≌△CFD(AAS),
∴EB=DF,
∴EB=AD.

 名校课堂系列答案
名校课堂系列答案【题目】在“一日捐”活动中,九(2)班42名同学捐款金额统计如下表,则在这次活动中,该班同学捐款金额的众数是( )
金额(元) | 20 | 30 | 35 | 50 | 100 | 150 |
学生数(名) | 5 | 7 | 9 | 13 | 5 | 3 |
A.3B.35C.50D.150