题目内容
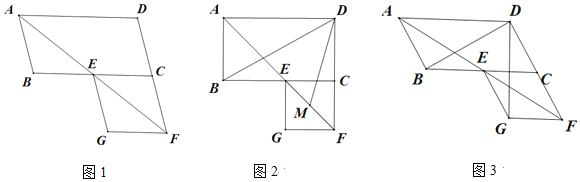
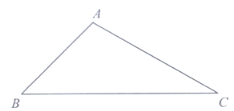
【题目】如图,平行四边形ABCD中,E是BC边上的一点,且AB=AE,若AE平分∠DAB,∠EAC=20°,则∠AED的度数为( )

A. 70°B. 75°C. 80°D. 85°
【答案】C
【解析】
先证明∠B=∠EAD,然后利用SAS证明△ABC≌△EAD,得出∠AED=∠BAC.再证明△ABE为等边三角形,可得∠BAE=60°,求出∠BAC的度数,即可得∠AED的度数.
∵在平行四边形ABCD中,AD∥BC,BC=AD,
∴∠EAD=∠AEB,
又∵AB=AE,
∴∠B=∠AEB,
∴∠B=∠EAD,
在△ABC和△EAD中,
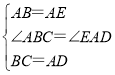 ,
,
∴△ABC≌△EAD(SAS),
∴∠AED=∠BAC.
∵AE平分∠DAB,
∴∠BAE=∠DAE,
∴∠BAE=∠AEB=∠B,
∴△ABE为等边三角形,
∴∠BAE=60°,
∴∠BAC=∠BAE+∠EAC=80°,
∴∠AED=∠BAC=80°;
故选C.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】有这样一个问题:探究函数y=![]() 的图象与性质。小慧根据学习函数的经验,对函数y=
的图象与性质。小慧根据学习函数的经验,对函数y=![]() 的图象与性质进行了探究。下面是小慧的探究过程,请补充完成:
的图象与性质进行了探究。下面是小慧的探究过程,请补充完成:
(1)函数y=![]() 的自变量x的取值范围是__________;
的自变量x的取值范围是__________;
(2)列出y与x的几组对应值。请直接写出m的值,m=________;
x | … | -3 | -2 | 0 | 1 | 1.5 | 2.5 | m | 4 | 6 | 7 | … |
y | … | 2.4 | 2.5 | 3 | 4 | 6 | -2 | 0 | 1 | 1.5 | 1.6 | … |
(3)请在平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点,并画出该函数的图象;
(4)结合函数的图象,写出该函数的两条性质:
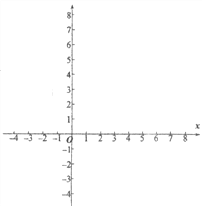
①_____________________________________________;
②____________________________________________。