题目内容
【题目】如图，以正方形
的顶点
为直角顶点，作等腰直角三角形
，连接
、
，当
、
、
三点在--条直线上时，若
，
，则正方形的面积是( )
A.
B.
C.
D.
【答案】C
【解析】
由“ASA”可证△ABF≌△CBE，可得AF=CE=3，由等腰直角三角形的性质可得BH=FH=1，由勾股定理可求BC2=5，即可求正方形ABCD的面积
解：∵四边形ABCD是正方形，△BEF是等腰直角三角形
∴AB=BC，BE=BF，∠ABC=∠EBF=90°，
∴∠ABF=∠EBC，且AB=BC，BE=BF
∴△ABF≌△CBE（SAS）
∴AF=CE=3
如图，过点BH⊥EC于H，
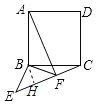
∵BE=BF=
，BH⊥EC
∴BH=FH=1
∴CH=EC-EH=2
∵BC2=BH2+CH2=5，
∴正方形ABCD的面积=5.
故选择：C.
练习册系列答案
相关题目
【题目】
年
月
日是第
个世界读书日，为迎接第个世界读书日的到来，某校举办读书分享大赛活动：大赛以“推荐分享”为主题，参赛者选择一本自己最喜欢的书，然后给该书写一段推荐语、一篇读书心得、举办一场读书讲座．大赛组委会对参赛者提交的推荐语、读书心得、举办的读书讲座进行打分（各项成绩均按百分制），综合成绩排名第一的选手将获得大赛一等奖．现有甲、乙两位同学的各项成绩如下表所示；
参赛者 | 推荐语 | 读书心得 | 读书讲座 |
甲 |
|
|
|
乙 |
|
|
|
（1）若将三项成绩的平均分作为参赛选手的综合成绩，则甲、乙二人谁最有可能获得大赛一等奖？请通过计算说明理由．
（2）若“推荐语”“读书心得”“读书讲座”的成绩按
确定综合成绩，则甲、乙二人谁最有可能获得大赛一等奖？请通过计算说明理由．
