题目内容
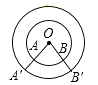
【题目】如图,大海中有两个岛屿A与B,在海岸线PQ上点E处测得∠AEP=74°,∠BEQ=30°,在点F处测得∠AFP=60°,∠BFQ=60°.
(1)判断AE,AB的数量关系,并说明理由;
(2)求∠BAE的度数.

【答案】(1)见解析;(2) 28°.
【解析】
(1)在△EOF中,根据三角形内角和定理得出∠EOF=90°.在△EBF中,根据外角的性质得出∠EBF=30°,根据等角对等边得到EF=BF,由等腰三角形三线合一的性质得到AF垂直平分BE,由线段垂直平分线的性质即可得到结论;
(2)由三角形外角的性质得出∠EAO的度数,再由等腰三角形三线合一的性质即可得到结论.
(1)AE=AB.理由如下:
∵∠BEF=30°,∠AFE=60°,∴∠EOF=90°.
∵∠BFQ=60°,∠BEF=30°,∴∠EBF=30°,∴BF=EF,∴OE=OB,即AF垂直平分BE,∴AE=AB;
(2)∵∠AEP=74°,∠AFP=60°,∴∠EAF=74°-60°=14°.
∵AE=AB,AF⊥BE,∴∠EAO=∠BAO,∴∠BAE=2∠EAO =2∠EAF=28°.

练习册系列答案
相关题目