题目内容
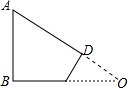
如图，四边形ABCD中，∠A=60°，∠B=∠D=90°，AB=4，CD=2，则BC=______．
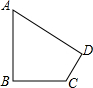
延长AD、BC交于O，
∵∠B=90°，∠A=60°，
∴∠O=30°，
∴OA=2AB=8，OC=2CD=4，
由勾股定理得：OB=
=4
，
∴BC=OB-OC=4
-4．
故答案为：4
-4．
∵∠B=90°，∠A=60°，
∴∠O=30°，
∴OA=2AB=8，OC=2CD=4，
由勾股定理得：OB=
| OA2-AB2 |
| 3 |
∴BC=OB-OC=4
| 3 |
故答案为：4
| 3 |
练习册系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
