题目内容
当a=4，b=2时
（1）分别求代数式①a2-2ab+b2及 ②（a-b）2的值．
（2）观察①、②两个代数式的值，你得到①和②之间有什么关系？
（3）利用（2）的结论，求当a=
，b=
时，a2-2ab+b2的值．
（1）分别求代数式①a2-2ab+b2及 ②（a-b）2的值．
（2）观察①、②两个代数式的值，你得到①和②之间有什么关系？
（3）利用（2）的结论，求当a=
| 1001 |
| 1000 |
| 501 |
| 1000 |
分析：（1）把a、b的值分别代入进行计算即可得解；
（2）根据计算结果可得两代数相等；
（3）把a、b的值代入（2）的结论进行计算即可得解．
（2）根据计算结果可得两代数相等；
（3）把a、b的值代入（2）的结论进行计算即可得解．
解答：解：（1）当a=4，b=2时，
①a2-2ab+b2
=42-2×4×2+22
=16-16+4
=4；
②（a-b）2=（4-2）2=4；
（2）a2-2ab+b2=（a-b）2；
（3）当a=
，b=
时，a2-2ab+b2=（a-b）2=（
-
）2=（
）2=
．
①a2-2ab+b2
=42-2×4×2+22
=16-16+4
=4；
②（a-b）2=（4-2）2=4；
（2）a2-2ab+b2=（a-b）2；
（3）当a=
| 1001 |
| 1000 |
| 501 |
| 1000 |
| 1001 |
| 1000 |
| 501 |
| 1000 |
| 1 |
| 2 |
| 1 |
| 4 |
点评：本题考查了代数式求值，把a、b的值代入代数式进行准确计算是解题的关键．
练习册系列答案
桃李文化快乐暑假武汉出版社系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
的路程y（km）与时间x（h）的函数图象如图所示．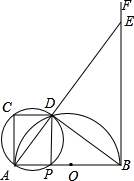
B重合），过A、P、C三点的圆与⊙O相交于除点A以外的另一点D，连接AD并延长交射线BF于点E，连接DB、DP、DC．
如图，在一个坡角为30°的斜坡上有一棵树，高AB，当太阳光与水平线成60°时，测得该树在斜坡上的树影BC的长为6m，则树高AB=
矩形ABCD的边长AB=6，BC=4，点F在DC上，DF=2．动点M、N分别从点D、B同时出发，沿线段DA、线段BA向点A的方向运动，当动点M运动到点A时，M、N两点同时停止运动．连接FM、FN．设点M、N的运动速度都是1个单位/秒，M、N运动的时间为x秒，问：当x为多少时，FM⊥FN？
抛物线上的一点C，使△OCA∽△OBC，且AC：BC=