题目内容
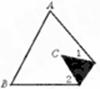
已知,如图所示,折叠长方形OABC的一边BC,使点B落在OA边的点D处,如果AB=8,BC=10,求E的坐标.


点E的坐标为(10,3)
试题分析:求点E的坐标,关键是求出AE的长度.本题是翻折中较复杂的计算,解题的关键是弄清翻折过程中对应线段与对应角,利用勾股定理求解所需线段.想求得AE长,先利用勾股定理计算出OD的长度,进而可求AD,而DE=BE,在Rt△ADE中利用勾股定理即可求得AE的长度,进而可得点E的坐标.
试题解析:
解:设AE的长为x,
∴BE=DE=8-x.
∵△CBE折叠后的图形是△CDE,
∴CB=CD=10,
∵在Rt△COD中:
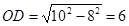
∴AD=10-6=4
∵在Rt△ADE中:
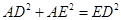
即:

解得:
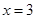
∴点E的坐标为(10,3)

练习册系列答案
 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目

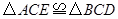 ;(2)
;(2)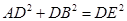 .
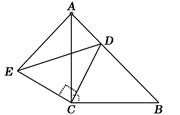
.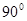 ,AD平分∠BAC,BC=10,BD=6,则点D到AB的距离是 .
,AD平分∠BAC,BC=10,BD=6,则点D到AB的距离是 .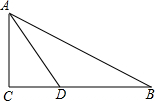
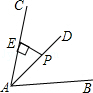
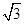 ,则它的斜边长为 .
,则它的斜边长为 .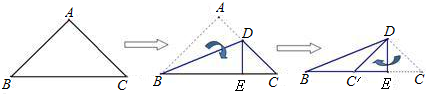
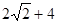 。
。