题目内容
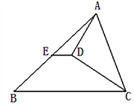
【题目】如图,在△ABC中,从A点向∠ACB的角平分线作垂线,垂足为D,E是AB的中点,已知AC=4,BC=6,则DE的长为( )
A. 1 B. ![]() C.
C. ![]() D. 2
D. 2
【答案】A
【解析】延长AD交BC于F,根据等腰三角形三线合一的性质求出AD=DF,然后判断出DE是△ABF的中位线,根据三角形的中位线平行于第三边并且等于第三边的一半求解即可.
解:如图,延长AD交BC于F,
∵CD是∠ACD的角平分线,CD⊥AD,
∴AD=DF,AC=CF,(等腰三角形三线合一),
又∵E是AB的中点,
∴DE是△ABF的中位线,
∴DE=![]() BF,
BF,
∵AC=4,BC=6,
∴BF=BC-CF=6-4=2,
∴DE=![]() ×2=1.
×2=1.
故选:A.
“点睛”本题考查了三角形的中位线平行于第三边并且等于第三边的一半,等腰三角形三线合一的性质,难点在作辅助线构造出一DE为中位线的三角形.

练习册系列答案
相关题目
【题目】某水果店卖出的香蕉数量(千克)与售价(元)之间的关系如下表:
香蕉数量(千克) | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | … |
售价(元) | 1.5 | 3 | 4.5 | 6 | 7.5 | 9 | 10.5 | … |
上表反映了两个变量之间的关系,其中,自变量是________,因变量是________.