题目内容
已知抛物线C1的函数解析式为y=ax2+bx-3a(b<0),若抛物线C1经过点(0,-3),方程ax2+bx-3a=0的两根为x1,x2,且|x1-x2|=4.(1)求抛物线C1的顶点坐标.
(2)已知实数x>0,请证明x+
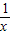 ≥2,并说明x为何值时才会有x+
≥2,并说明x为何值时才会有x+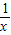 =2.
=2.(3)若将抛物线先向上平移4个单位,再向左平移1个单位后得到抛物线C2,设A(m,y1),B(n,y2)是C2上的两个不同点,且满足:∠AOB=90°,m>0,n<0.请你用含m的表达式表示出△AOB的面积S,并求出S的最小值及S取最小值时一次函数OA的函数解析式.
(参考公式:在平面直角坐标系中,若P(x1,y1),Q(x2,y2),则P,Q两点间的距离为
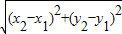 )
)
【答案】分析:(1)求抛物线的顶点坐标,需要先求出抛物线的解析式,即确定待定系数a、b的值.已知抛物线图象与y轴交点,可确定解析式中的常数项(由此得到a的值);然后从方程入手求b的值,题干给出了两根差的绝对值,将其进行适当变形(转化为两根和、两根积的形式),结合根与系数的关系即可求出b的值.
(2)x•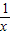 =1,因此将x+
=1,因此将x+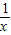 配成完全平方式,然后根据平方的非负性即可得证.
配成完全平方式,然后根据平方的非负性即可得证.
(3)结合(1)的抛物线的解析式以及函数的平移规律,可得出抛物线C2的解析式;在Rt△OAB中,由勾股定理可确定m、n的关系式,然后用m列出△AOB的面积表达式,结合不等式的相关知识可确定△OAB的最小面积值以及此时m的值,进而由待定系数法确定一次函数OA的解析式.
解答:解:(1)∵抛物线过(0,-3)点,∴-3a=-3
∴a=1
∴y=x2+bx-3
∵x2+bx-3=0的两根为x1,x2且|x1-x2|=4
∴|x1-x2|=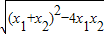 =4,且b<0
=4,且b<0
∴b=-2
∴y=x2-2x-3=(x-1)2-4
∴抛物线C1的顶点坐标为(1,-4).
(2)∵x>0,∴x+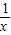 -2=(
-2=(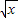 -
-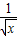 )2≥0
)2≥0
∴x+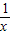 ≥2,显然当x=1时,才有x+
≥2,显然当x=1时,才有x+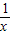 =2.
=2.
(3)由平移知识易得C2的解析式为:y=x2
∴A(m,m2),B(n,n2)
∵△AOB为直角三角形,
∴OA2+OB2=AB2
∴m2+m4+n2+n4=(m-n)2+(m2-n2)2
化简得:m n=-1
∴S△AOB=
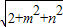 =
=
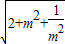
=
 =
= (m+
(m+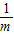 )≥
)≥ •2=1
•2=1
∴S△AOB的最小值为1,此时m=1,A(1,1)
∴直线OA的一次函数解析式为y=x.
点评:该题考查了二次函数解析式的确定、函数图象的平移、不等式的应用等知识,解题过程中完全平方式的变形被多次提及,应熟练掌握并能灵活应用.
(2)x•
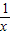 =1,因此将x+
=1,因此将x+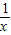 配成完全平方式,然后根据平方的非负性即可得证.
配成完全平方式,然后根据平方的非负性即可得证.(3)结合(1)的抛物线的解析式以及函数的平移规律,可得出抛物线C2的解析式;在Rt△OAB中,由勾股定理可确定m、n的关系式,然后用m列出△AOB的面积表达式,结合不等式的相关知识可确定△OAB的最小面积值以及此时m的值,进而由待定系数法确定一次函数OA的解析式.
解答:解:(1)∵抛物线过(0,-3)点,∴-3a=-3
∴a=1
∴y=x2+bx-3
∵x2+bx-3=0的两根为x1,x2且|x1-x2|=4
∴|x1-x2|=
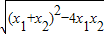 =4,且b<0
=4,且b<0∴b=-2
∴y=x2-2x-3=(x-1)2-4
∴抛物线C1的顶点坐标为(1,-4).
(2)∵x>0,∴x+
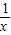 -2=(
-2=(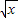 -
-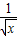 )2≥0
)2≥0∴x+
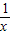 ≥2,显然当x=1时,才有x+
≥2,显然当x=1时,才有x+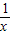 =2.
=2.(3)由平移知识易得C2的解析式为:y=x2
∴A(m,m2),B(n,n2)
∵△AOB为直角三角形,
∴OA2+OB2=AB2
∴m2+m4+n2+n4=(m-n)2+(m2-n2)2
化简得:m n=-1
∴S△AOB=

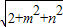 =
=
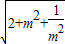
=

 =
= (m+
(m+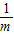 )≥
)≥ •2=1
•2=1∴S△AOB的最小值为1,此时m=1,A(1,1)
∴直线OA的一次函数解析式为y=x.
点评:该题考查了二次函数解析式的确定、函数图象的平移、不等式的应用等知识,解题过程中完全平方式的变形被多次提及,应熟练掌握并能灵活应用.

练习册系列答案
相关题目
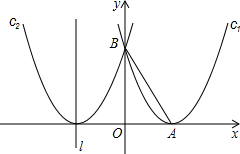 已知,如图所示,抛物线c1:y=ax2+bx+c的顶点A在x轴的正半轴上,并与y轴交于点B,OA=
已知,如图所示,抛物线c1:y=ax2+bx+c的顶点A在x轴的正半轴上,并与y轴交于点B,OA=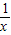 ≥2,并说明x为何值时才会有x+
≥2,并说明x为何值时才会有x+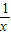 =2.
=2.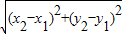 )
)