题目内容
己知:二次函数y=ax2+bx+6(a≠0)与x轴交于A、B两点(点A在点B的左侧),点A、点B的横坐标是一元二次方程x2-4x-12=0的两个根.
(1)请直接写出点A、点B的坐标.
(2)请求出该二次函数表达式及对称轴和顶点坐标.
(3)如图1,在二次函数对称轴上是否存在点P,使△APC的周长最小,若存在,请求出点P的坐标;若不存在,请说明理由.
(4)如图2,连接AC、BC,点Q是线段0B上一个动点(点Q不与点0、B重合).过点Q作QD∥AC交BC于点D,设Q点坐标(m,0),当△CDQ面积S最大时,求m的值.

(1)请直接写出点A、点B的坐标.
(2)请求出该二次函数表达式及对称轴和顶点坐标.
(3)如图1,在二次函数对称轴上是否存在点P,使△APC的周长最小,若存在,请求出点P的坐标;若不存在,请说明理由.
(4)如图2,连接AC、BC,点Q是线段0B上一个动点(点Q不与点0、B重合).过点Q作QD∥AC交BC于点D,设Q点坐标(m,0),当△CDQ面积S最大时,求m的值.

(1)A(-2,0),B(6,0);
(2)将A、B两点坐标代入二次函数y=ax2+bx+6,得
,
解得
,
∴y=-
x2+2x+6,
∵y=-
(x-2)2+8,
∴抛物线对称轴为x=2,顶点坐标为(2,8);
(3)如图,作点C关于抛物线对称轴的对称点C′,连接AC′,交抛物线对称轴于P点,连接CP,
∵C(0,6),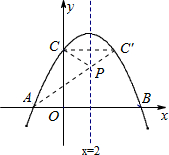
∴C′(4,6),设直线AC′解析式为y=ax+b,则
,
解得
,
∴y=x+2,当x=2时,y=4,
即P(2,4);
(4)依题意,得AB=8,QB=6-m,AQ=m+2,OC=6,则S△ABC=
AB×OC=24,
∵由DQ∥AC,∴△BDQ∽△BCA,
∴
=(
)2=(
)2,
即S△BDQ=
(m-6)2,
又S△ACQ=
AQ×OC=3m+6,
∴S=S△ABC-S△BDQ-S△ACQ=24-
(m-6)2-(3m+6)=-
m2+
m+
=-
(m-2)2+6,
∴当m=2时,S最大.
(2)将A、B两点坐标代入二次函数y=ax2+bx+6,得
|
解得
|
∴y=-
| 1 |
| 2 |
∵y=-
| 1 |
| 2 |
∴抛物线对称轴为x=2,顶点坐标为(2,8);
(3)如图,作点C关于抛物线对称轴的对称点C′,连接AC′,交抛物线对称轴于P点,连接CP,
∵C(0,6),

∴C′(4,6),设直线AC′解析式为y=ax+b,则
|
解得
|
∴y=x+2,当x=2时,y=4,
即P(2,4);
(4)依题意,得AB=8,QB=6-m,AQ=m+2,OC=6,则S△ABC=
| 1 |
| 2 |
∵由DQ∥AC,∴△BDQ∽△BCA,
∴
| S△BDQ |
| S△BCA |
| BQ |
| BA |
| 6-m |
| 8 |
即S△BDQ=
| 3 |
| 8 |
又S△ACQ=
| 1 |
| 2 |
∴S=S△ABC-S△BDQ-S△ACQ=24-
| 3 |
| 8 |
| 3 |
| 8 |
| 3 |
| 2 |
| 9 |
| 2 |
| 3 |
| 8 |
∴当m=2时,S最大.

练习册系列答案
相关题目
 的长是方程x2-6x+5=0的两个实数根.
的长是方程x2-6x+5=0的两个实数根.


 ,0),顶点为P.
,0),顶点为P.
