题目内容
若一个多边形的内角和为1440°，则这个多边形的边数为________，对角线的条数为________，外角和为________．
10 35 360°
分析：多边形的内角和可以表示成（n-2）•180°，依此列方程可求多边形的边数；再由多边形的对角线公式求出对角线的条数；而多边形的外角和是固定的360°．
解答：设所求正n边形边数为n，
则1440°=（n-2）•180°，
解得n=10；
十边形的对角线共有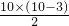
=35条；
十边形的外角和为360°．
点评：本题考查多边形的内角和与外角和定理以及一个n边形共有
条对角线．
分析：多边形的内角和可以表示成（n-2）•180°，依此列方程可求多边形的边数；再由多边形的对角线公式求出对角线的条数；而多边形的外角和是固定的360°．
解答：设所求正n边形边数为n，
则1440°=（n-2）•180°，
解得n=10；
十边形的对角线共有
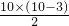=35条；十边形的外角和为360°．
点评：本题考查多边形的内角和与外角和定理以及一个n边形共有
条对角线． 
练习册系列答案
相关题目