题目内容

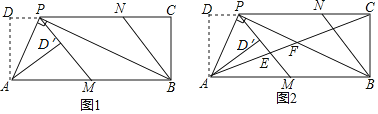
【题目】如图，在四边形ABCD中，已知AB＝CD，M、N、P分别是AD、BC、BD的中点∠ABD＝20°，∠BDC＝70°，则∠NMP的度数为（　　）

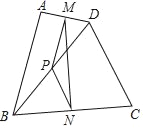
A. 50° B. 25° C. 15° D. 20

【答案】B

【解析】

根据中位线定理和已知，易证明△PMN是等腰三角形，根据等腰三角形的性质和已知条件即可求出∠PMN的度数．

在四边形ABCD中，∵M、N、P分别是AD、BC、BD的中点，∴PN，PM分别是△CDB与△DAB的中位线，∴PMAB，PNDC，PM∥AB，PN∥DC．

∵AB=CD，∴PM=PN，∴△PMN是等腰三角形，∴∠PMN=∠PNM．

∵PM∥AB，PN∥DC，∴∠MPD=∠ABD=20°，∠BPN=∠BDC=70°，∴∠MPN=∠MPD+∠NPD=20°+（180﹣70）°=130°，∴∠PMN25°．

故选B．

练习册系列答案
相关题目

【题目】如图，在平面直角坐标系中，直线与轴， 轴分别交于点A、B，抛物线经过点A和点B，与x轴的另一个交点为C，动点D从点A出发，以每秒1个单位长度的速度向O点运动，同时动点E从点B出发，以每秒2个单位长度的速度向A点运动，设运动的时间为t秒，0﹤t﹤5.

（1）求抛物线的解析式；

（2）当t为何值时，以A、D、E为顶点的三角形与△AOB相似；

（3）当△ADE为等腰三角形时，求t的值；

（4）抛物线上是否存在一点F，使得以A、B、D、F为顶点的四边形是平行四边形？若存在，直接写出F点的坐标；若不存在，说明理由.

【题目】如图，四边形ABCD的四个顶点分别在反比例函数与(x＞0，0＜m＜n)的图象上，对角线BD//y轴，且BD⊥AC于点P．已知点B的横坐标为4．

（1）当m=4，n=20时．

①若点P的纵坐标为2，求直线AB的函数表达式．

②若点P是BD的中点，试判断四边形ABCD的形状，并说明理由．

（2）四边形ABCD能否成为正方形？若能，求此时m，n之间的数量关系；若不能，试说明理由．

【题目】如图1，在矩形ABCD中，P为CD边上一点（DP＜CP），∠APB=90°．将△ADP沿AP翻折得到△AD′P，PD′的延长线交边AB于点M，过点B作BN∥MP交DC于点N．

（1）求证：AD2=DPPC；

（2）请判断四边形PMBN的形状，并说明理由；

（3）如图2，连接AC，分别交PM，PB于点E，F．若=，求的值．

【题目】如图，在Rt△ABC中，∠C＝90°，以AC为直径作⊙O，交AB于D．

(1)在图(1)中，用直尺和圆规过点D作⊙O的切线DE交BC于点E；(保留作图痕迹，不写作法)

(2)如图(2)，如果⊙O的半径为3，ED＝4，延长EO交⊙O于F，连接DF，与OA交于点G，求OG的长．

【题目】《九章算术》是我国古代数学的经典著作，书中有一个问题：“今有黄金九枚，白银一十一枚，称之重适等，交易其一，金轻十三两，问金、银一枚各重几何？”意思是：甲袋中装有黄金9枚（每枚黄金重量相同），乙袋中装有白银11枚（每枚白银重量相同），称重两袋相同，两袋互相交换1枚后，甲袋比乙袋轻了13两（袋子重量忽略不计），问黄金、白银每枚各种多少两？设黄金重两，每枚白银重两，根据题意可列方程组为____.

【题目】如图，在Rt△ABC中，∠C＝90°，∠B＝30°，BC＝3，点D是BC边上一动点（不与B，C重合），过点D做DE⊥BC交AB于点E，将∠B沿着直线DE翻折，点B落在BC边上的点F处，若∠AFE＝90°，则BD的长是_____．

【题目】如图，PB为⊙O的切线，B为切点，过B作OP的垂线BA，垂足为C，交⊙O于点A，连接PA、AO，并延长AO交⊙O于点E，与PB的延长线交于点D．

（1）求证：PA是⊙O的切线；（2）若AC＝6，OC＝4，求PA的长．

【题目】（本小题满分10分）如图，在Rt△ABC中，∠ABC=90°，AC的垂直平分线分别与AC，BC及AB的延长线相交于点D，E，F，且BF=BC．⊙O是△BEF的外接圆，∠EBF的平分线交EF于点G，交于点H，连接BD、FH．

（1）求证：△ABC≌△EBF；

（2）试判断BD与⊙O的位置关系，并说明理由；

（3）若AB=1，求HGHB的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网