题目内容
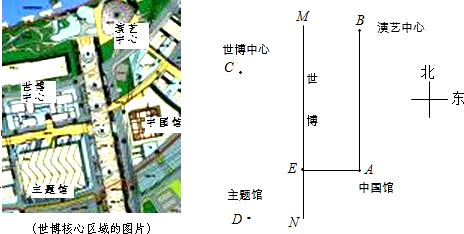
小明是世博志愿者,前不久到世博园区参观.园区的核心区域“一轴四馆”(如左图所示)引起了他的关注.小明发现,世博轴大致上为南北走向,演艺中心在中国馆的正北方向,世博中心在中国馆的北偏西45°方向,且演艺中心、世博中心到中国馆的距离相等.从中国馆出发向西走大约200米,到达世博轴上的点E处,这时测得世博中心在北偏西26.6°方向.小明把该核心区域抽象成右侧的示意图(图中只显示了部分信息).(1)把题中的数据在示意图上标出,有关信息用几何语言加以描述(如AB∥MN等);
(2)试求出中国馆与演艺中心的距离(精确到1米).
(备用数据:sin26.6°=0.45,cos26.6°=0.9,tan26.6°=0.5,
 ).
).
【答案】分析:(1)根据方向角的定义即可确定;
(2)过点C作CH⊥AB垂足为点H,则△AHC是等腰三角形,再在直角△CFE中利用三角函数即可得到一个关于AH的方程,即可求得AH的长度,进而求得AC的长.
解答: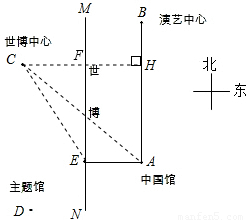 解:(1)如图,AB∥MN,AB=AC,AE⊥MN,AE=200,
解:(1)如图,AB∥MN,AB=AC,AE⊥MN,AE=200,
∠BAC=45°,∠MEC=26.6°,
(2)过点C作CH⊥AB垂足为点H,交MN于点F,
∵∠BAC=45°,
∴CH=AH,FH=AE=200.
设AH=CH=x,则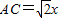 ,CF=x-200,
,CF=x-200,
∴在Rt△CFE中,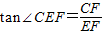 ,
,
∴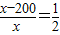 ,
,
解得x=400.
则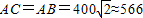 米.
米.
点评:本题主要考查了三角形的计算,一般的三角形可以通过作高线转化为解直角三角形的计算,计算时首先计算直角三角形的公共边是常用的思路.
(2)过点C作CH⊥AB垂足为点H,则△AHC是等腰三角形,再在直角△CFE中利用三角函数即可得到一个关于AH的方程,即可求得AH的长度,进而求得AC的长.
解答:
 解:(1)如图,AB∥MN,AB=AC,AE⊥MN,AE=200,
解:(1)如图,AB∥MN,AB=AC,AE⊥MN,AE=200,∠BAC=45°,∠MEC=26.6°,
(2)过点C作CH⊥AB垂足为点H,交MN于点F,
∵∠BAC=45°,
∴CH=AH,FH=AE=200.
设AH=CH=x,则
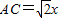 ,CF=x-200,
,CF=x-200,∴在Rt△CFE中,
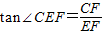 ,
,∴
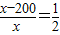 ,
,解得x=400.
则
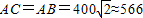 米.
米.点评:本题主要考查了三角形的计算,一般的三角形可以通过作高线转化为解直角三角形的计算,计算时首先计算直角三角形的公共边是常用的思路.

练习册系列答案
相关题目
 ).
).
 ).
).
 ).
).