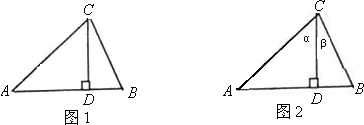题目内容
课题研究(1)如图(1),我们已经学习了直角三角形中的边角关系,在Rt△ACD中,sin∠A=______,所以CD=______,而S△ABC=
 AB•CD,于是可将三角形面积公式变形,得S△ABC=______.①其文字语言表述为:三角形的面积等于两边及其夹角正弦积的一半.这就是我们将要在高中学习的正弦定理.
AB•CD,于是可将三角形面积公式变形,得S△ABC=______.①其文字语言表述为:三角形的面积等于两边及其夹角正弦积的一半.这就是我们将要在高中学习的正弦定理.(2)如图(2),在△ABC中,CD⊥AB于D,∠ACD=α,∠DCB=β.
∵S△ABC=S△ADC+S△BDC,由公式①,得
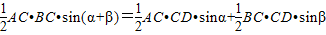 ,即
,即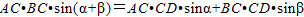 ②.
②.请你利用直角三角形边角关系,消去②中的AC、BC、CD,将得到新的结论.并写出解决过程.
(3)利用(2)中的结论,试求sin75°和sin105°的值,并比较其大.
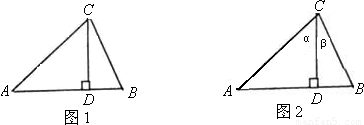
【答案】分析:(1)根据锐角三角函数的概念进行填空即可;
(2)结合等式的性质和锐角三角函数的概念进行转换;
(3)利用(2)中的结论,把75°和105°拆分成特殊角即可计算.
解答:解.(1)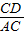 ,ACsinA,
,ACsinA,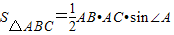 ;
;
(2)把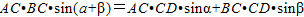
两边同除以AC•BC,得

在Rt△BCD和Rt△ACD中分别可得:
cosα=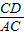 ,cosβ=
,cosβ=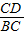 ,
,
∴sin(α+β)=sinα•cosβ+cosα•sinβ;
(3)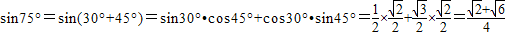
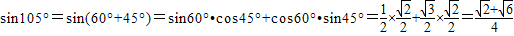
由此可见:sin75°=sin105°.
点评:掌握锐角三角函数的概念,熟记特殊角的锐角三角函数值.
(2)结合等式的性质和锐角三角函数的概念进行转换;
(3)利用(2)中的结论,把75°和105°拆分成特殊角即可计算.
解答:解.(1)
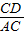 ,ACsinA,
,ACsinA,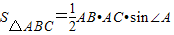 ;
;(2)把
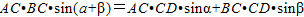
两边同除以AC•BC,得

在Rt△BCD和Rt△ACD中分别可得:
cosα=
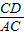 ,cosβ=
,cosβ=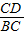 ,
,∴sin(α+β)=sinα•cosβ+cosα•sinβ;
(3)
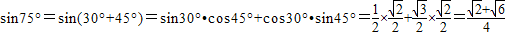
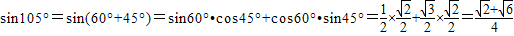
由此可见:sin75°=sin105°.
点评:掌握锐角三角函数的概念,熟记特殊角的锐角三角函数值.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
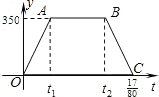 沪杭高速铁路已开工建设,某校研究性学习以此为课题,在研究列车的行驶速度时,得到一个数学问题.如图,若v是关于t的函数,图象为折线O-A-B-C,其中A(t1,350),B(t2,350),C(
沪杭高速铁路已开工建设,某校研究性学习以此为课题,在研究列车的行驶速度时,得到一个数学问题.如图,若v是关于t的函数,图象为折线O-A-B-C,其中A(t1,350),B(t2,350),C(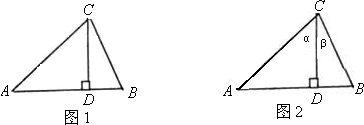
 AB•CD,于是可将三角形面积公式变形,得S△ABC=______.①其文字语言表述为:三角形的面积等于两边及其夹角正弦积的一半.这就是我们将要在高中学习的正弦定理.
AB•CD,于是可将三角形面积公式变形,得S△ABC=______.①其文字语言表述为:三角形的面积等于两边及其夹角正弦积的一半.这就是我们将要在高中学习的正弦定理.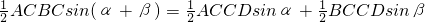 ,即
,即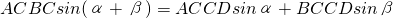 ②.
②.