Question

在平面直角坐标系中，一蚂蚁从原点O出发，按向上、向右、向下、向右的方向依次不断移动，每次移动1个单位．其行走路线如图所示．

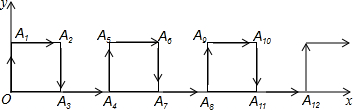
（1）填写下列各点的坐标：A₄（______，______），A₈（______，______），A₁₀（______，______），A₁₂（______，______）；
（2）写出点A_4n的坐标（n是正整数）；
（3）按此移动规律，若点A_m在x轴上，请用含n的代数式表示m（n是正整数）；
（4）指出蚂蚁从点A₂₀₁₁到点A₂₀₁₂的移动方向．

Answer 1

解：（1）由图可知，A₄，A₁₂，A₈都在x轴上，
∵小蚂蚁每次移动1个单位，
∴OA₄=2，OA₈=4，OA₁₂=6，
∴A₄（2，0），A₈（4，0），A₁₂（6，0）；
同理可得出：A₁₀（5，1），；
故答案为：2，0；4，0；5，1；6，0；

（2）根据（1）OA_4n=4n÷2=2n，
∴点A_4n的坐标（2n，0）；

（3）∵只有下表为4的倍数或比4n小1的数在x轴上，
∴点A_m在x轴上，用含n的代数式表示为：m=4n或m=4n-1；

（4）∵2011÷4=502…3，
∴从点A₂₀₁₁到点A₂₀₁₂的移动方向与从点A₃到A₄的方向一致，为向右．
分析：（1）观察图形可知，A₄，A₈都在x轴上，求出OA₄、OA₈的长度，然后写出坐标即可；
（2）根据（1）中规律写出点A_4n的坐标即可；
（3）根据以上所求即可得出在x轴上点的变化规律以及下标为4n或4n-1，进而得出答案；
（4）根据2011÷4=502..3，可知从点A₂₀₁₁到点A₂₀₁₂的移动方向与从点A₃到A₄的方向一致．
点评：此题主要考查了点的变化规律，比较简单，仔细观察图形，确定出A_4n都在x轴上是解题的关键．