题目内容
如图,直线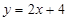 与
与 轴交于点
轴交于点 ,与
,与 轴交于点
轴交于点 .点
.点 在
在 轴上,且
轴上,且 ,在此平面上,存在点
,在此平面上,存在点 ,使得四边形
,使得四边形 恰好为平行四边形.
恰好为平行四边形.

(1)求点 的坐标;
的坐标;
(2)求所有满足条件的 点坐标.
点坐标.
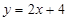 与
与 轴交于点
轴交于点 ,与
,与 轴交于点
轴交于点 .点
.点 在
在 轴上,且
轴上,且 ,在此平面上,存在点
,在此平面上,存在点 ,使得四边形
,使得四边形 恰好为平行四边形.
恰好为平行四边形.
(1)求点
 的坐标;
的坐标;(2)求所有满足条件的
 点坐标.
点坐标.(1)(4,0)或(-4,0);(2) 或
或
 或
或
试题分析:(1)先求出直线与坐标轴的交点坐标,再结合
 即可得到结果;
即可得到结果;(2)根据平行四边形的对边平行可得
 //
// 轴,即可得到点
轴,即可得到点 的纵坐标,再根据平行四边形的对边相等可得点
的纵坐标,再根据平行四边形的对边相等可得点 的横坐标,从而求得结果.
的横坐标,从而求得结果.(1)在
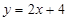 中,当
中,当 时,
时, ,当
,当 时,
时,
∴
 点坐标为
点坐标为 ;
; 点坐标
点坐标
设
 点坐标为
点坐标为 
∵

∴

∴
 点坐标分别为
点坐标分别为 或
或 ;
;(2)假设存在点
 ,使四边形
,使四边形 恰好为平行四边形
恰好为平行四边形∴
 //
// 轴,
轴,∴点
 与点
与点 纵坐标相等,即
纵坐标相等,即
当
 时,
时,
∴

当
 时,
时,
∴

综上所述,当点
 的坐标为
的坐标为 、
、 时,四边形
时,四边形 恰好为平行四边形.
恰好为平行四边形.点评:解答本题的关键是熟练掌握
 轴上的点的纵坐标为0,y轴上的点的横坐标为0;平行于x轴的直线上的点的纵坐标相等.
轴上的点的纵坐标为0,y轴上的点的横坐标为0;平行于x轴的直线上的点的纵坐标相等.
练习册系列答案
相关题目
 经过点(
经过点( ,
, )和点(
)和点( ,
, ).
). 的图象相交于点P(1,2),则这个一次函数图象的解析式是( ).
的图象相交于点P(1,2),则这个一次函数图象的解析式是( ). 





 的图象与x轴的交点坐标为 ,与y轴的交点坐标为 .
的图象与x轴的交点坐标为 ,与y轴的交点坐标为 . 的描述,下列说法正确的是( )
的描述,下列说法正确的是( )
 随
随 的增大而增大
的增大而增大 的图像不经过第三象限,那么
的图像不经过第三象限,那么 的取值范围为
的取值范围为