题目内容
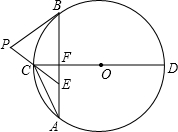 如图,已知⊙O的弦AB垂直于直径CD,垂足为F,点E在AB上,且EA=EC.
如图,已知⊙O的弦AB垂直于直径CD,垂足为F,点E在AB上,且EA=EC.(1)求证:AC2=AE•AB;
(2)延长EC到点P,连接PB,若PB=PE,试判断PB与⊙O的位置关系,并说明理由.
分析:(1)要求证:AC2=AE•AB,只要证明△AEC∽△ACB即可;
(2)判断PB为⊙O的切线,只要证明PB⊥OB即可.
(2)判断PB为⊙O的切线,只要证明PB⊥OB即可.
解答: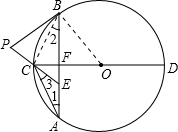 (1)证明:连接BC,
(1)证明:连接BC,
∵AB⊥CD,CD为⊙O的直径,
∴BC=AC.
∴∠1=∠2.
又∵AE=CE,
∴∠1=∠3.
∴△AEC∽△ACB.
∴
=
.
即AC2=AB•AE.(4分)
(2)解:PB与⊙O相切.理由如下:
连接OB,
∵PB=PE,
∴∠PBE=∠PEB.
∵∠1=∠2=∠3,
∴∠PEB=∠1+∠3=2∠2.
∵∠PBE=∠2+∠PBC,∴∠PBC=∠2,
∵∠OBC=∠OCB.
∴∠OBP=∠OBC+∠PBC=∠OCB+∠2=90°.
∴PB⊥OB.
即PB为⊙O的切线.(10分)
 (1)证明:连接BC,
(1)证明:连接BC,∵AB⊥CD,CD为⊙O的直径,
∴BC=AC.
∴∠1=∠2.
又∵AE=CE,
∴∠1=∠3.
∴△AEC∽△ACB.
∴
| AC |
| AB |
| AE |
| AC |
即AC2=AB•AE.(4分)
(2)解:PB与⊙O相切.理由如下:
连接OB,
∵PB=PE,
∴∠PBE=∠PEB.
∵∠1=∠2=∠3,
∴∠PEB=∠1+∠3=2∠2.
∵∠PBE=∠2+∠PBC,∴∠PBC=∠2,
∵∠OBC=∠OCB.
∴∠OBP=∠OBC+∠PBC=∠OCB+∠2=90°.
∴PB⊥OB.
即PB为⊙O的切线.(10分)
点评:证明线段的乘积相等的问题一般可以转化为三角形相似问题,证明切线的问题,可以转化为证明切线是垂直于半径,并且经过半径的外端点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知⊙O的弦AB、CD相交于点E,
如图,已知⊙O的弦AB、CD相交于点E, |
| AC |
 |
| BD |
| A、60° | B、100° |
| C、80° | D、130° |
 如图,已知⊙O的弦AB、CD相交于点P,PA=4cm,PB=3cm,PC=6cm,EA切⊙O于点A,AE与CD的延长线交于点E,若AE=2
如图,已知⊙O的弦AB、CD相交于点P,PA=4cm,PB=3cm,PC=6cm,EA切⊙O于点A,AE与CD的延长线交于点E,若AE=2| 5 |
| A、4cm | ||
| B、3cm | ||
| C、5cm | ||
D、
|
 如图,已知⊙O的弦CD垂直于直径AB,点E在CD上,且EC=EB.
如图,已知⊙O的弦CD垂直于直径AB,点E在CD上,且EC=EB. 23、如图,已知⊙O的弦AB垂直于直径CD,垂足为F,连接CA、CB.
23、如图,已知⊙O的弦AB垂直于直径CD,垂足为F,连接CA、CB. 如图,已知⊙O的弦AC=2cm,∠ABC=45°,则图中阴影部分的面积是
如图,已知⊙O的弦AC=2cm,∠ABC=45°,则图中阴影部分的面积是