题目内容
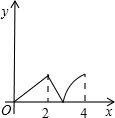
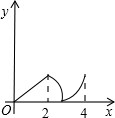
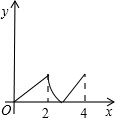
 如图,菱形ABCD中,∠A=60°,AB=2,动点P从点B出发,以每秒1个单位长度的速度沿B→C→D向终点D运动.同时动点Q从点A出发,以相同的速度沿A→D→B向终点B运动,运动的时间为x秒,当点P到达点D时,点P、Q同时停止运动,设△APQ的面积为y,则反映y与x的函数关系的图象是( )
如图,菱形ABCD中,∠A=60°,AB=2,动点P从点B出发,以每秒1个单位长度的速度沿B→C→D向终点D运动.同时动点Q从点A出发,以相同的速度沿A→D→B向终点B运动,运动的时间为x秒,当点P到达点D时,点P、Q同时停止运动,设△APQ的面积为y,则反映y与x的函数关系的图象是( )分析:分0≤x<2时;2≤x<3,3≤x≤4三种情况,利用三角形的面积公式分别用含x的代数式表示S△AQP,然后根据求得的解析式得到对应的函数图象即可得到答案.
解答:解:∵菱形ABCD中,∠A=60°,AB=2,
∴DB=2.
①当0≤x<2时,过Q作QH⊥AB于H,
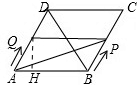
∵AQ=BP=x,
∴PQ=AB=2,
而∠A=60°,
∴QH=
x,
∴S△AQP=
•2•
x=
x;
它的函数图象为射线;
②当2≤x<3,如图,
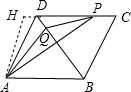
过A作AH⊥DC于D,则AH=
,
DQ=x-2,PC=x-2,DP=4-x,
S△APQ=S△ADP-S△ADQ-S△PDQ
=
•
(4-x)-
•2•(x-2)•
-
•(x-2)(4-x)•
=
(x-5)2-
,
它的函数图象为抛物线对称轴左侧的一部分,并且开口向上,
③当3≤x≤4,如图,
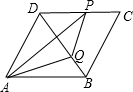
S△APQ=S△ADQ+S△PDQ-S△ADP=
•2•(x-2)•
+-
•(x-2)(4-x)•
-
•
(4-x)=-
(x-5)2+
,
它的函数图象为抛物线对称轴左侧的一部分,并且开口向下;
所以选项A正确.
故选A.
∴DB=2.
①当0≤x<2时,过Q作QH⊥AB于H,

∵AQ=BP=x,
∴PQ=AB=2,
而∠A=60°,
∴QH=
| ||
| 2 |
∴S△AQP=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
它的函数图象为射线;
②当2≤x<3,如图,

过A作AH⊥DC于D,则AH=
| 3 |
DQ=x-2,PC=x-2,DP=4-x,
S△APQ=S△ADP-S△ADQ-S△PDQ
=
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
5
| ||
| 4 |
它的函数图象为抛物线对称轴左侧的一部分,并且开口向上,
③当3≤x≤4,如图,

S△APQ=S△ADQ+S△PDQ-S△ADP=
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| ||
| 4 |
5
| ||
| 4 |
它的函数图象为抛物线对称轴左侧的一部分,并且开口向下;
所以选项A正确.
故选A.
点评:本题考查了利用分类讨论的思想求动点问题的函数图象;也考查了三角形的面积公式以及一次函数和二次函数的图象.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
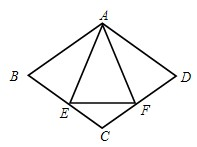 26、已知:如图,菱形ABCD中,E,F分别是CB,CD上的点,且BE=DF.
26、已知:如图,菱形ABCD中,E,F分别是CB,CD上的点,且BE=DF.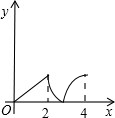
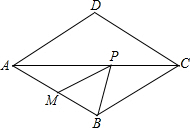 如图,菱形ABCD中,∠BAD=60°,M是AB的中点,P是对角线AC上的一个动点,若AB长为2
如图,菱形ABCD中,∠BAD=60°,M是AB的中点,P是对角线AC上的一个动点,若AB长为2 如图:菱形ABCD中,E是AB的中点,且CE⊥AB,AB=6cm.
如图:菱形ABCD中,E是AB的中点,且CE⊥AB,AB=6cm. 如图,菱形ABCD中,∠ADC=120°,AB=10,
如图,菱形ABCD中,∠ADC=120°,AB=10,