题目内容
（2013•贺州）如图，在△ABC中，∠ABC=45°，AC=8cm，F是高AD和BE的交点，则BF的长是（ ）分析：求出∠FBD=∠CAD，AD=BD，证△DBF≌△DAC，推出BF=AC，代入求出即可．
解答：解：∵F是高AD和BE的交点，
∴∠ADC=∠ADB=∠AEF=90°，
∴∠CAD+∠AFE=90°，∠DBF+∠BFD=90°，
∵∠AFE=∠BFD，
∴∠CAD=∠FBD，
∵∠ADB=90°，∠ABC=45°，
∴∠BAD=45°=∠ABD，
∴AD=BD，
在△DBF和△DAC中
∴△DBF≌△DAC（ASA），
∴BF=AC=8cm，
故选C．
∴∠ADC=∠ADB=∠AEF=90°，
∴∠CAD+∠AFE=90°，∠DBF+∠BFD=90°，
∵∠AFE=∠BFD，
∴∠CAD=∠FBD，
∵∠ADB=90°，∠ABC=45°，
∴∠BAD=45°=∠ABD，
∴AD=BD，
在△DBF和△DAC中
|
∴△DBF≌△DAC（ASA），
∴BF=AC=8cm，
故选C．
点评：本题考查了等腰三角形的性质，全等三角形的性质和判定，三角形的内角和定理的应用，关键是推出△DBF≌△DAC．
练习册系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
（2013•贺州）如图是一个几何体的三视图，根据图中提供的数据（单位：cm）可求得这个几何体的体积为（ ）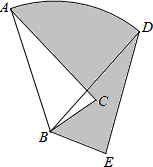
（2013•贺州）如图，在△ABC中，AB=6，将△ABC绕点B顺时针旋转60°后得到△DBE，点A经过的路径为弧AD，则图中阴影部分的面积是
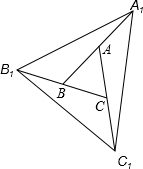（2013•贺州）如图，A、B、C分别是线段A1B，B1C，C1A的中点，若△ABC的面积是1，那么△A1B1C1的面积
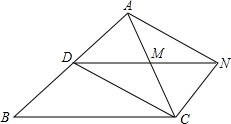（2013•贺州）如图，D是△ABC的边AB上一点，CN∥AB，DN交AC于点M，若MA=MC．