题目内容
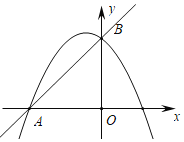
【题目】拋物线![]() 分别交
分别交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
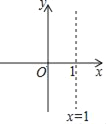
轴于点![]() .抛物线的对称轴
.抛物线的对称轴![]() 与
与![]() 轴相交于点
轴相交于点![]() ,直线
,直线![]() 与抛物线的对称轴
与抛物线的对称轴![]() 相交于点
相交于点![]() .
.
(1)直接写出抛物线的解折式和点![]() 的坐标;
的坐标;
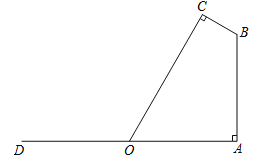
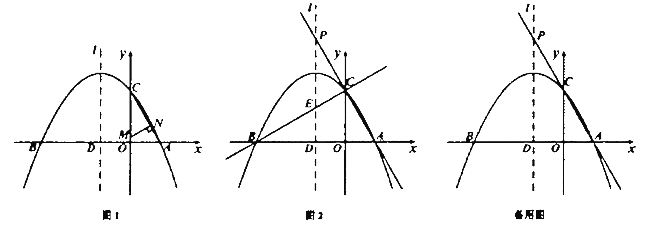
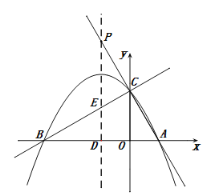
(2)如图1,点![]() 为线段
为线段![]() 上的动点,点
上的动点,点![]() 为线段
为线段![]() 上的动点,且
上的动点,且![]() .在点
.在点![]() ,点
,点![]() 移动的过程中,
移动的过程中,![]() 是否有最小值?如果有,请求出最小值;
是否有最小值?如果有,请求出最小值;
(3)以点![]() 为旋转中心,将直线
为旋转中心,将直线![]() 绕点
绕点![]() 逆时针旋转,旋转角为
逆时针旋转,旋转角为![]() (
(![]() ),直线
),直线![]() 旋转时,与抛物线的对称轴
旋转时,与抛物线的对称轴![]() 相交于点
相交于点![]() ,与抛物线的另一个交点为点
,与抛物线的另一个交点为点![]() .
.
①如图2,当直线![]() 旋转到与直线
旋转到与直线![]() 重合时,判断线段
重合时,判断线段![]() 的数量关系?并说明理由
的数量关系?并说明理由
②当![]() 为等腰三角形时,请直按写出点
为等腰三角形时,请直按写出点![]() 的坐标.
的坐标.
【答案】(1)![]() ,
,![]() ;(2)有最小值,
;(2)有最小值,![]() ;(3)①
;(3)①![]() ,见解析;②
,见解析;②![]() 的坐标分别为
的坐标分别为![]() ,
,![]() .
.
【解析】
⑴用待定系数法可得抛物线的解析式为:![]() ; 根据对称轴求法
; 根据对称轴求法![]() ,可得
,可得![]() .
.
⑵根据三角函数即可解得;
⑶①设直线![]() 的解析式为
的解析式为![]() ,由待定系数法可得直线
,由待定系数法可得直线![]() 的解析式为,再根据三角函数即可得到答案;
的解析式为,再根据三角函数即可得到答案;
②根据等腰三角形的性质即可得到答案.
解:⑴因为拋物线![]() 分别交
分别交![]() 轴于点
轴于点![]() ,用待定系数法可得
,用待定系数法可得
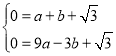 ,解得
,解得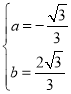 抛物线的解析式为:
抛物线的解析式为:![]() ;
;
由抛物线的对称轴![]() 与
与![]() 轴相交于点
轴相交于点![]() ,根据对称轴求法
,根据对称轴求法![]() ,可得
,可得![]() .
.
⑵在![]() 移动的过程中,
移动的过程中,![]() 有最小值.
有最小值.
∵![]()
∴在![]() 中,
中,![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,
,
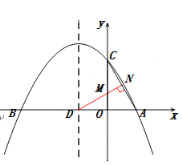
根据垂线段最短,![]() 的长就是
的长就是![]() 的最小值.
的最小值.
∵![]() ,
,![]() ,∴
,∴![]()
∴在![]() 中,
中,![]() .
.
⑶①![]()
理由如下:设直线![]() 的解析式为
的解析式为![]()
将![]() ,
,![]() 代入
代入![]()
于是得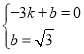 ,解得
,解得 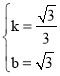
∴直线![]() 的解析式为
的解析式为![]() ,
,
∵点![]() ,∴点
,∴点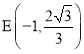 ,∴
,∴![]()
∵![]() ,∴
,∴![]()
∴在![]() 中,由⑵得,
中,由⑵得,![]()
∴![]() ,∴
,∴![]() ,
,
∴![]()
∴![]() .
.
②当![]() 为等腰三角形时点
为等腰三角形时点![]() 的坐标分别为
的坐标分别为![]() ,
,![]() .
.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目