题目内容
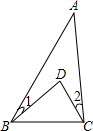如图，已知∠1=20゜，∠2=25゜，∠A=35゜，求∠BDC的度数．分析：先根据三角形内角和定理得到∠1+∠DBC+∠2+∠DCB+∠A=180°，则可计算出∠DBC+∠DCB=100゜，然后再在△BDC中利用三角形内角和定理计算∠BDC的度数．
解答：解：在△ABC中，
∵∠A+∠ABC+∠ACB=180゜，即∠1+∠DBC+∠2+∠DCB+∠A=180°，
∴∠DBC+∠DCB=180゜-20゜-25゜-35゜=100゜，
∴∠BDC=180°-（∠DBC+∠DCB）=80゜．
∵∠A+∠ABC+∠ACB=180゜，即∠1+∠DBC+∠2+∠DCB+∠A=180°，
∴∠DBC+∠DCB=180゜-20゜-25゜-35゜=100゜，
∴∠BDC=180°-（∠DBC+∠DCB）=80゜．
点评：本题考查了三角形内角和定理：三角形内角和是180°．
练习册系列答案
相关题目
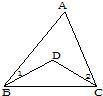17、如图，已知∠1=20°，∠2=25°，∠A=35°，则∠BDC（小于平角）的度数为
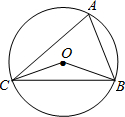（2012•六盘水）如图，已知∠OCB=20°，则∠A=
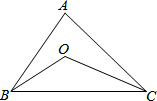如图，已知∠ABO=20°，∠ACO=25°，∠A=55°，则∠BOC等于（ ）
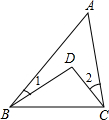如图，已知∠1=20°，∠2=25°，∠A=50°，则∠BDC的度数是