ΧβΡΩΡΎ»ί
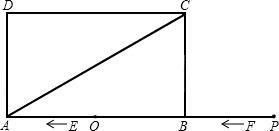 »γΆΦΘ§ΨΊ–ΈABCD÷–Θ§AB=6Θ§BC=2
»γΆΦΘ§ΨΊ–ΈABCD÷–Θ§AB=6Θ§BC=2| 3 |
Θ®1Θ©Β±Β»±ΏΓςEFGΒΡ±ΏFG«ΓΚΟΨ≠ΙΐΒψC ±Θ§«σ‘ΥΕ· ±ΦδtΒΡ÷ΒΘΜ
Θ®2Θ©‘Ύ’ϊΗω‘ΥΕ·Ιΐ≥Χ÷–Θ§…ηΒ»±ΏΓςEFGΚΆΨΊ–ΈABCD÷ΊΒΰ≤ΩΖ÷ΒΡΟφΜΐΈΣSΘ§«κ÷±Ϋ”–¥≥ωS”κt÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΚΆœύ”ΠΒΡΉ‘±δΝΩtΒΡ»Γ÷ΒΖΕΈßΘΜ
Θ®3Θ©…ηEG”κΨΊ–ΈABCDΒΡΕ‘Ϋ«œΏACΒΡΫΜΒψΈΣHΘ§ «Ζώ¥φ‘Ύ’β―υΒΡtΘ§ ΙΓςAOH «Β»―ϋ»ΐΫ«–ΈΘΩ»τ¥φ‘ΎΘ§«σ≥ωΕ‘”ΠΒΡtΒΡ÷ΒΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
Ζ÷ΈωΘΚΘ®1Θ©Β±±ΏFG«ΓΚΟΨ≠ΙΐΒψC ±Θ§ΓœCFB=60ΓψΘ§BF=3-tΘ§‘ΎRtΓςCBF÷–Θ§Ϋβ÷±Ϋ«»ΐΫ«–ΈΩ…«σtΒΡ÷ΒΘΜ
Θ®2Θ©Α¥’’Β»±ΏΓςEFGΚΆΨΊ–ΈABCD÷ΊΒΰ≤ΩΖ÷ΒΡΆΦ–ΈΧΊΒψΘ§Ζ÷ΈΣ0ΓήtΘΦ1Θ§1ΓήtΘΦ3Θ§3ΓήtΘΦ4Θ§4ΓήtΘΦ6ΥΡ÷÷«ιΩωΘ§Ζ÷±π–¥≥ωΚ· ΐΙΊœΒ ΫΘΜ
Θ®3Θ©¥φ‘ΎΘ°Β±ΓςAOH «Β»―ϋ»ΐΫ«–Έ ±Θ§Ζ÷ΈΣAH=AO=3Θ§HA=HOΘ§OH=OA»ΐ÷÷«ιΩωΘ§Ζ÷±πΜ≠≥ωΆΦ–ΈΘ§ΗυΨίΧΊ β»ΐΫ«–ΈΒΡ–‘÷ Θ§Ν–ΖΫ≥Χ«σtΒΡ÷ΒΘ°
Θ®2Θ©Α¥’’Β»±ΏΓςEFGΚΆΨΊ–ΈABCD÷ΊΒΰ≤ΩΖ÷ΒΡΆΦ–ΈΧΊΒψΘ§Ζ÷ΈΣ0ΓήtΘΦ1Θ§1ΓήtΘΦ3Θ§3ΓήtΘΦ4Θ§4ΓήtΘΦ6ΥΡ÷÷«ιΩωΘ§Ζ÷±π–¥≥ωΚ· ΐΙΊœΒ ΫΘΜ
Θ®3Θ©¥φ‘ΎΘ°Β±ΓςAOH «Β»―ϋ»ΐΫ«–Έ ±Θ§Ζ÷ΈΣAH=AO=3Θ§HA=HOΘ§OH=OA»ΐ÷÷«ιΩωΘ§Ζ÷±πΜ≠≥ωΆΦ–ΈΘ§ΗυΨίΧΊ β»ΐΫ«–ΈΒΡ–‘÷ Θ§Ν–ΖΫ≥Χ«σtΒΡ÷ΒΘ°
Ϋβ¥πΘΚΫβΘΚΘ®1Θ©Β±±ΏFG«ΓΚΟΨ≠ΙΐΒψC ±Θ§ΓœCFB=60ΓψΘ§BF=3-tΘ§‘ΎRtΓςCBF÷–Θ§BC=2
Θ§tanΓœCFB=
Θ§
Φ¥tan60Γψ=
Θ§Φ¥
=
Θ§
ΫβΒΟt=1Θ§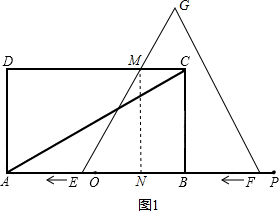
ΓύΒ±±ΏFG«ΓΚΟΨ≠ΙΐΒψC ±Θ§t=1ΘΜ
Θ®2Θ©»γΆΦ1Θ§ΙΐΒψMΉςMNΓΆAB”ΎΒψNΘ§
Β±0ΓήtΘΦ1 ±Θ§
ΓΏtan60Γψ=
=
=
Θ§
ΓύEN=2Θ§
EB=3+tȧNB=3+t-2=1+tȧ
ΓύMC=1+tΘ§
S=
Θ®MC+EBΘ©ΓΝBC=2
t+4
ΘΜ
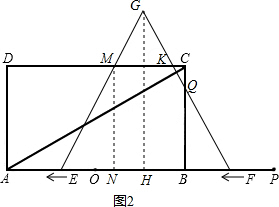
»γΆΦ2Θ§Β±1ΓήtΘΦ3 ±Θ§
ΓΏMN=2
Θ§EF=OP=6Θ§
ΓύGH=6ΓΝ
=3
Θ§
Γύ
=
Θ§
ΓύMK=2Θ§
ÿEB=3+tȧBF=3-tȧBQ=
BF=
Θ®3-tΘ©Θ§
CQ=2
-BQ=
t-
Θ§
ΓύS=SΧί–ΈMKFE-SΓςQBF=-
t2+3
t+
ΘΜ
Β±3ΓήtΘΦ4 ±Θ§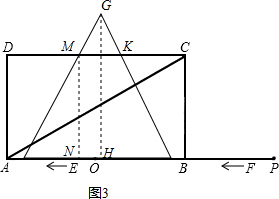
ΓΏMN=2
ȧEF=6-2Ȯt-3ȩ=12-2tȧ
ΓύGH=Θ®12-2tΘ©ΓΝ
=6
-
tȧ
Γύ
=
Θ§
ΓύMK=8-2tΘ§
S=-4
t+20
ΘΜ
»γΆΦ4Θ§Β±4ΓήtΘΦ6 ±Θ§
ÿEF=12-2tȧ
ΗΏΈΣΘΚEF•sin60Γψ=
EFΘ§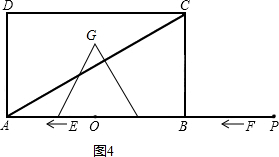
S=
t2-12
t+36
ΘΜ
Ήέ…œΥυ ωΘ§S=
ΘΜ
Θ®3Θ©¥φ‘ΎΘ°
άμ”…»γœ¬ΘΚ‘ΎRtΓςABC÷–Θ§tanΓœCAB=
=
Θ§
ΓύΓœCAB=30ΓψΘ§
”÷ΓΏΓœHEO=60ΓψΘ§
ΓύΓœHAE=ΓœAHE=30ΓψΘ§
ΓύAE=HE=3-tΜρt-3Θ§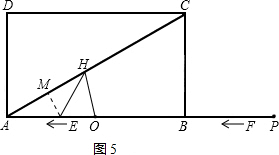
1Θ©Β±AH=AO=3 ±Θ§Θ®»γΆΦ5Θ©Θ§ΙΐΒψEΉςEMΓΆAH”ΎMΘ§
‘ρAM=
AH=
Θ§
‘ΎRtΓςAME÷–Θ§cosΓœMAE=
Θ§
Φ¥cos30Γψ=
Θ§
ΓύAE=
Θ§Φ¥3-t=
Μρt-3=
Θ§
Γύt=3-
Μρt=3+
Θ§
2Θ©Β±HA=HO ±Θ§Θ®»γΆΦ6Θ©‘ρΓœHOA=ΓœHAO=30ΓψΘ§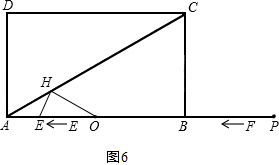
”÷ΓΏΓœHEO=60ΓψΘ§
ΓύΓœEHO=90ΓψΘ§EO=2HE=2AEΘ§
”÷ΓΏAE+EO=3Θ§
ΓύAE+2AE=3Θ§AE=1Θ§
Φ¥3-t=1Μρt-3=1Θ§
Γύt=2Μρt=4ΘΜ
3Θ©Β±OH=OA ±Θ§Θ®»γΆΦ7Θ©Θ§‘ρΓœOHA=ΓœOAH=30ΓψΘ§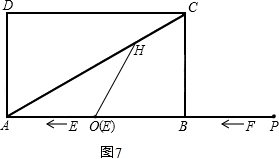
ΓύΓœHOB=60Γψ=ΓœHEBΘ§
ΓύΒψEΚΆΒψO÷ΊΚœΘ§
ΓύAE=AO=3Θ§
Β±EΗ’ΩΣ Φ‘ΥΕ· ±3-t=3Θ§
Β±ΒψEΖΒΜΊO ± «ΘΚt-3=3Θ§
Φ¥3-t=3Μρt-3=3Θ§t=6Θ®…α»ΞΘ©Μρt=0ΘΜ
Ήέ…œΥυ ωΘ§¥φ‘Ύ5Ηω’β―υΒΡt÷ΒΘ§ ΙΓςAOH «Β»―ϋ»ΐΫ«–ΈΘ§Φ¥t=3-
Μρt=3+
Μρt=2Μρt=4Μρt=0Θ°
| 3 |
| BC |
| BF |
Φ¥tan60Γψ=
2
| ||
| 3-t |
| 3 |
2
| ||
| 3-t |
ΫβΒΟt=1Θ§

ΓύΒ±±ΏFG«ΓΚΟΨ≠ΙΐΒψC ±Θ§t=1ΘΜ
Θ®2Θ©»γΆΦ1Θ§ΙΐΒψMΉςMNΓΆAB”ΎΒψNΘ§
Β±0ΓήtΘΦ1 ±Θ§
ΓΏtan60Γψ=
| MN |
| EN |
2
| ||
| NE |
| 3 |
ΓύEN=2Θ§
EB=3+tȧNB=3+t-2=1+tȧ
ΓύMC=1+tΘ§
S=
| 1 |
| 2 |
| 3 |
| 3 |

»γΆΦ2Θ§Β±1ΓήtΘΦ3 ±Θ§
ΓΏMN=2
| 3 |
ΓύGH=6ΓΝ
| ||
| 2 |
| 3 |
Γύ
| MK |
| EF |
| GH-MN |
| GH |
ΓύMK=2Θ§
ÿEB=3+tȧBF=3-tȧBQ=
| 3 |
| 3 |
CQ=2
| 3 |
| 3 |
| 3 |
ΓύS=SΧί–ΈMKFE-SΓςQBF=-
| ||
| 2 |
| 3 |
7
| ||
| 2 |
Β±3ΓήtΘΦ4 ±Θ§

ΓΏMN=2
| 3 |
ΓύGH=Θ®12-2tΘ©ΓΝ
| ||
| 2 |
| 3 |
| 3 |
Γύ
| MK |
| EF |
| GH-MN |
| GH |
ΓύMK=8-2tΘ§
S=-4
| 3 |
| 3 |
»γΆΦ4Θ§Β±4ΓήtΘΦ6 ±Θ§
ÿEF=12-2tȧ
ΗΏΈΣΘΚEF•sin60Γψ=
| ||
| 2 |

S=
| 3 |
| 3 |
| 3 |
Ήέ…œΥυ ωΘ§S=
|
Θ®3Θ©¥φ‘ΎΘ°
άμ”…»γœ¬ΘΚ‘ΎRtΓςABC÷–Θ§tanΓœCAB=
| BC |
| AB |
| ||
| 3 |
ΓύΓœCAB=30ΓψΘ§
”÷ΓΏΓœHEO=60ΓψΘ§
ΓύΓœHAE=ΓœAHE=30ΓψΘ§
ΓύAE=HE=3-tΜρt-3Θ§

1Θ©Β±AH=AO=3 ±Θ§Θ®»γΆΦ5Θ©Θ§ΙΐΒψEΉςEMΓΆAH”ΎMΘ§
‘ρAM=
| 1 |
| 2 |
| 3 |
| 2 |
‘ΎRtΓςAME÷–Θ§cosΓœMAE=
| AM |
| AE |
Φ¥cos30Γψ=
| ||
| AE |
ΓύAE=
| 3 |
| 3 |
| 3 |
Γύt=3-
| 3 |
| 3 |
2Θ©Β±HA=HO ±Θ§Θ®»γΆΦ6Θ©‘ρΓœHOA=ΓœHAO=30ΓψΘ§

”÷ΓΏΓœHEO=60ΓψΘ§
ΓύΓœEHO=90ΓψΘ§EO=2HE=2AEΘ§
”÷ΓΏAE+EO=3Θ§
ΓύAE+2AE=3Θ§AE=1Θ§
Φ¥3-t=1Μρt-3=1Θ§
Γύt=2Μρt=4ΘΜ
3Θ©Β±OH=OA ±Θ§Θ®»γΆΦ7Θ©Θ§‘ρΓœOHA=ΓœOAH=30ΓψΘ§

ΓύΓœHOB=60Γψ=ΓœHEBΘ§
ΓύΒψEΚΆΒψO÷ΊΚœΘ§
ΓύAE=AO=3Θ§
Β±EΗ’ΩΣ Φ‘ΥΕ· ±3-t=3Θ§
Β±ΒψEΖΒΜΊO ± «ΘΚt-3=3Θ§
Φ¥3-t=3Μρt-3=3Θ§t=6Θ®…α»ΞΘ©Μρt=0ΘΜ
Ήέ…œΥυ ωΘ§¥φ‘Ύ5Ηω’β―υΒΡt÷ΒΘ§ ΙΓςAOH «Β»―ϋ»ΐΫ«–ΈΘ§Φ¥t=3-
| 3 |
| 3 |
ΒψΤάΘΚ±ΨΧβΩΦ≤ιΝΥΧΊ β»ΐΫ«–ΈΓΔΨΊ–ΈΒΡ–‘÷ Θ§œύΥΤ»ΐΫ«–ΈΒΡ≈–Ε®”κ–‘÷ Θ§Ϋβ÷±Ϋ«»ΐΫ«–ΈΒΡ”–ΙΊ÷Σ ΕΘ°ΙΊΦϋ «ΗυΨίΧΊ β»ΐΫ«–ΈΒΡ–‘÷ Θ§Ζ÷άύΧ÷¬έΘ°

ΝΖœΑ≤αœΒΝ–¥πΑΗ
œύΙΊΧβΡΩ
 »γΆΦΘ§ΨΊ–ΈABCD÷–Θ§AD=aΘ§AB=bΘ§“Σ ΙBC±Ώ…œ÷Ν…Ό¥φ‘Ύ“ΜΒψPΘ§ ΙΓςABPΓΔΓςAPDΓΔΓςCDPΝΫΝΫœύΥΤΘ§‘ρaΓΔbΦδΒΡΙΊœΒ Ϋ“ΜΕ®¬ζΉψΘ®ΓΓΓΓΘ©
»γΆΦΘ§ΨΊ–ΈABCD÷–Θ§AD=aΘ§AB=bΘ§“Σ ΙBC±Ώ…œ÷Ν…Ό¥φ‘Ύ“ΜΒψPΘ§ ΙΓςABPΓΔΓςAPDΓΔΓςCDPΝΫΝΫœύΥΤΘ§‘ρaΓΔbΦδΒΡΙΊœΒ Ϋ“ΜΕ®¬ζΉψΘ®ΓΓΓΓΘ©AΓΔaΓί
| ||
| BΓΔaΓίb | ||
CΓΔaΓί
| ||
| DΓΔaΓί2b |
 »γΆΦΘ§ΨΊ–ΈABCD÷–Θ§AB=6Θ§BC=8Θ§M «BCΒΡ÷–ΒψΘ§DEΓΆAMΘ§E «¥ΙΉψΘ§‘ρΓςABMΒΡΟφΜΐΈΣ
»γΆΦΘ§ΨΊ–ΈABCD÷–Θ§AB=6Θ§BC=8Θ§M «BCΒΡ÷–ΒψΘ§DEΓΆAMΘ§E «¥ΙΉψΘ§‘ρΓςABMΒΡΟφΜΐΈΣ 7ΓΔ»γΆΦΘ§ΨΊ–ΈABCD÷–Θ§AEΓΆBDΘ§¥ΙΉψΈΣEΘ§ΓœDAE=2ΓœBAEΘ§‘ρΓœCAE=
7ΓΔ»γΆΦΘ§ΨΊ–ΈABCD÷–Θ§AEΓΆBDΘ§¥ΙΉψΈΣEΘ§ΓœDAE=2ΓœBAEΘ§‘ρΓœCAE= Θ®2008•Μ≥»α«χΕΰΡΘΘ©“―÷Σ»γΆΦΘ§ΨΊ–ΈABCD÷–Θ§AB=3cmΘ§BC=4cmΘ§E «±ΏAD…œ“ΜΒψΘ§«“BE=EDΘ§P «Ε‘Ϋ«œΏ…œ»Έ“β“ΜΒψΘ§PFΓΆBEΘ§PGΓΆADΘ§¥ΙΉψΖ÷±πΈΣFΓΔGΘ°‘ρPF+PGΒΡ≥ΛΈΣ
Θ®2008•Μ≥»α«χΕΰΡΘΘ©“―÷Σ»γΆΦΘ§ΨΊ–ΈABCD÷–Θ§AB=3cmΘ§BC=4cmΘ§E «±ΏAD…œ“ΜΒψΘ§«“BE=EDΘ§P «Ε‘Ϋ«œΏ…œ»Έ“β“ΜΒψΘ§PFΓΆBEΘ§PGΓΆADΘ§¥ΙΉψΖ÷±πΈΣFΓΔGΘ°‘ρPF+PGΒΡ≥ΛΈΣ Θ®2002•Ές≤ΊΘ©“―÷ΣΘΚ»γΆΦΘ§ΨΊ–ΈABCD÷–Θ§EΓΔF «AB±Ώ…œΝΫΒψΘ§«“AF=BEΘ§Ν§ΫαDEΓΔCFΒΟΒΫΧί–ΈEFCDΘ°
Θ®2002•Ές≤ΊΘ©“―÷ΣΘΚ»γΆΦΘ§ΨΊ–ΈABCD÷–Θ§EΓΔF «AB±Ώ…œΝΫΒψΘ§«“AF=BEΘ§Ν§ΫαDEΓΔCFΒΟΒΫΧί–ΈEFCDΘ°