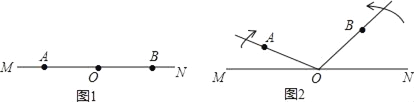题目内容
【题目】将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起(其中∠A=60°,∠D=30°,∠E=∠B=45°).
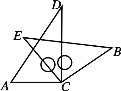
(1)猜想∠ACB与∠DCE的数量关系,并说明理由.
(2)当∠ACE<180°且点E在直线AC的上方时,这两块三角尺是否存在一组边互相平行?若存在,请直接写出∠ACE所有可能的度数及对应情况下的平行线(不必说明理由);若不存在,请说明理由.
【答案】(1)∠ACB+∠DCE=180°,理由见解析;(2)存在. 当∠ACE=30°时,AD∥BC;当∠ACE=45°时,AC∥BE;当∠ACE=120°时,AD∥CE;当∠ACE=135°时,BE∥CD;当∠ACE=165°时,BE∥AD.
【解析】
(1)由∠ACB=∠ACD+∠DCB,∠ACB+∠DCE=90°+∠DCB+∠DCE可得出结论;(2)分∠ACE=30°,45°,120°,135°及165°进行解答.
(1)∠ACB+∠DCE=180°,理由是:
∵∠ACB=∠ACD+∠DCB=90°+∠DCB
∴∠ACB+∠DCE=90°+∠DCB+∠DCE=90°+90°=180°
(2)存在. 当∠ACE=30°时,AD∥BC,理由如下,如图1所示:

∵∠ACE=∠DCB=30°,∠D=30°,
∴∠DCB=∠D,
∴AD∥BC;
当∠ACE=∠E=45°时,AC∥BE,理由如下,如图2所示:
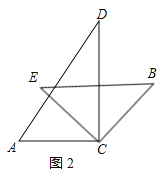
∵∠ACE=∠DCB=45°,∠B=45°,
∴BE⊥CD,
又∵AC⊥CD,
∴AC∥BE;
当∠ACE=120°时,AD∥CE,理由如下,如图3所示: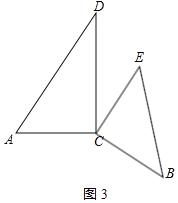
∵∠ACE=120°,
∴∠DCE=120°-90°=30°,
又∵∠D=30°,
∴∠DCE=∠D,
∴AD∥CE;
当∠ACE=135°时,BE∥CD,理由如下,如图4所示:
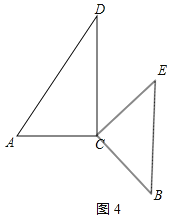
∵∠ACE=135°,
∴∠DCE=135°-90°=45°,
∵∠E=45°,
∴∠DCE=∠E,
∴BE∥CD;
当∠ACE=165°时,BE∥AD.理由如下:
延长AC交BE于F,如图5所示:
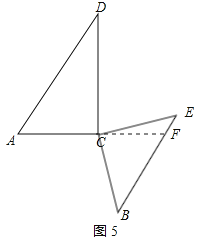
∵∠ACE=165°,
∴∠ECF=15°,
∵∠E=45°,
∴∠CFB=∠ECF+∠E=60°,
∵∠A=60°,
∴∠A=∠CFB,
∴BE∥AD.

 阅读快车系列答案
阅读快车系列答案【题目】在数学课上,同学们已经探究过“经过已知直线外一点作这条直线的垂线”的尺规作图过程:
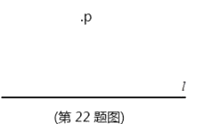
已知:直线
求作:直线 做法:如图:(1)在直线 (2)分别以点 (3)作直线 |
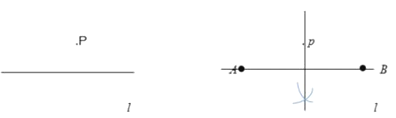
参考以上材料作图的方法,解决以下问题:
(1)以上材料作图的依据是 .
(3)已知:直线![]() 和
和![]() 外一点
外一点![]() ,
,
求作:![]() ,使它与直线
,使它与直线![]() 相切。(尺规作图,不写做法,保留作图痕迹,并把作图痕迹用黑色签字笔描黑)
相切。(尺规作图,不写做法,保留作图痕迹,并把作图痕迹用黑色签字笔描黑)