题目内容
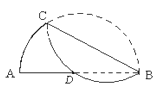
【题目】如图,将弧BC沿弦BC折叠交直径AB于点D,若AD=6, DB=7,则BC的长是()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
连接CA、CD,根据翻折的性质可得弧CD所对的圆周角是∠CBD,再根据AC弧所得的圆周角也是∠CBA,然后求出AC=CD,过点C作CE⊥AB于E,根据等腰三角形三线合一的性质可得AE=ED=![]() AD,根据直径所对的圆周角是直角可得∠ACB=90°,然后求出△ACE和△CBE相似,根据相似三角形对应边成比例求出CE2,再求出BE,然后利用勾股定理列式计算即可求出BC.
AD,根据直径所对的圆周角是直角可得∠ACB=90°,然后求出△ACE和△CBE相似,根据相似三角形对应边成比例求出CE2,再求出BE,然后利用勾股定理列式计算即可求出BC.
如图,连接CA、CD,

根据折叠的性质,弧CD所对的圆周角是∠CBD,
∵弧AC所对的圆周角是∠CBA,∠CBA=∠CBD,
∴AC=CD(相等的圆周角所对的弦相等),
过点C作CE⊥AB于E,
则AE=ED=![]() AD=
AD=![]() ×6=3,
×6=3,
∴BE=BD+DE=7+3=10,
∵AB是直径,
∴∠ACB=90°,
∵CE⊥AB,
∴∠ACB=∠AEC=90°,
∴∠A+∠ACE=∠ACE+∠BCE=90°,
∴∠A=∠BCE,
∴△ACE∽△CBE,
∴![]() ,
,
即CE2=AEBE=3×10=30,
在Rt△BCE中,BC=![]() =
=![]() =
=![]() ,
,
故选:D.

练习册系列答案
相关题目