题目内容
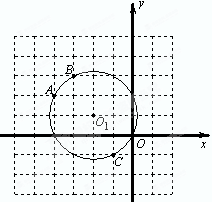
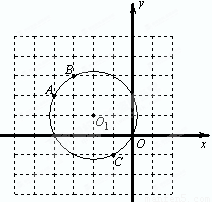
 已知⊙O1经过A(-4,2)、B(-3,3)、C(-1,-1)、O(0,0)四点,一次函数y=-x-2的图象是直线l,直线l与y轴交于点D.
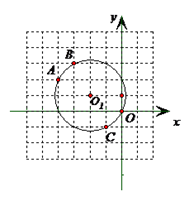
已知⊙O1经过A(-4,2)、B(-3,3)、C(-1,-1)、O(0,0)四点,一次函数y=-x-2的图象是直线l,直线l与y轴交于点D.(1)在如图的平面直角坐标系中画出直线l,则直线l与⊙O1的交点坐标为
(-4,2),(-1,1)
(-4,2),(-1,1)
;(2)若⊙O1上存在点P,使得△APD为等腰三角形,则这样的点P有
3
3
个,试写出其中一个点P坐标为(-3,-1)或(0,2)
(-3,-1)或(0,2)
.分析:(1)要先在坐标系上找到这些点,再画过这些点的图象;
(2)根据垂直平分线上的两点到线段两端的距离相等.作AD的垂直平分线,与圆的交点且是整点的点的坐标就是所求的坐标.当AD=PD时,该点也满足条件.
(2)根据垂直平分线上的两点到线段两端的距离相等.作AD的垂直平分线,与圆的交点且是整点的点的坐标就是所求的坐标.当AD=PD时,该点也满足条件.
解答: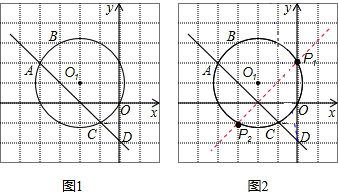 解:(1)先在坐标系中找到A(-4,2),B(-3,3),
解:(1)先在坐标系中找到A(-4,2),B(-3,3),
C(-1,-1),O(0,0)的坐标,然后画圆,过此四点.
一次函数y=-x-2,当x=0时,y=-2;
当y=0时,x=-2,从坐标系中先找出这两点,画过这两点的直线.
即是一次函数y=-x-2的图象.
该直线与圆的交点是点A、C,它们的坐标分别是(-4,2)、(-1,-1);
故答案是:(-4,2)、(-1,-1);
(2)作AD的垂直平分线,与圆的交点是所求的坐标(根据垂直平分线上的两点到线段两端的距离相等),以点D为圆心,以DA为半径画弧,弧与⊙O1的交点是A点和P3点,从图中可以看出这样的点有两个坐标分别是(-3,-1)或(0,2).
故答案是:3;(-3,-1)或(0,2).
 解:(1)先在坐标系中找到A(-4,2),B(-3,3),
解:(1)先在坐标系中找到A(-4,2),B(-3,3),C(-1,-1),O(0,0)的坐标,然后画圆,过此四点.
一次函数y=-x-2,当x=0时,y=-2;
当y=0时,x=-2,从坐标系中先找出这两点,画过这两点的直线.
即是一次函数y=-x-2的图象.
该直线与圆的交点是点A、C,它们的坐标分别是(-4,2)、(-1,-1);
故答案是:(-4,2)、(-1,-1);
(2)作AD的垂直平分线,与圆的交点是所求的坐标(根据垂直平分线上的两点到线段两端的距离相等),以点D为圆心,以DA为半径画弧,弧与⊙O1的交点是A点和P3点,从图中可以看出这样的点有两个坐标分别是(-3,-1)或(0,2).
故答案是:3;(-3,-1)或(0,2).
点评:本题考查了圆的综合题.以网格作为载体,将圆的直观性见于图形的直观性基础之上.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
 已知⊙O1经过A(-4,2),B(-3,3),C(-1,-1),O(0,0)四点,一次函数y=-x-2的图象是直线l,直线l与y轴交于点D.
已知⊙O1经过A(-4,2),B(-3,3),C(-1,-1),O(0,0)四点,一次函数y=-x-2的图象是直线l,直线l与y轴交于点D.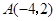 ,
,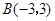 ,
,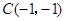 ,
,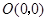 四点,一次函数
四点,一次函数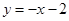 的图象是直线
的图象是直线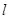 ,直线
,直线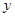 轴交于点
轴交于点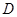 .
.
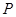 (横坐标与纵坐标均为整数的点称
(横坐标与纵坐标均为整数的点称 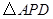 为等腰三角形,所有满足条件的点
为等腰三角形,所有满足条件的点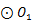 沿X轴向右平移 个单位时,
沿X轴向右平移 个单位时,