题目内容
(2013•怀化)已知函数y=kx2-2x+
(k是常数)
(1)若该函数的图象与x轴只有一个交点,求k的值;
(2)若点M(1,k)在某反比例函数的图象上,要使该反比例函数和二次函数y=kx2-2x+
都是y随x的增大而增大,求k应满足的条件以及x的取值范围;
(3)设抛物线y=kx2-2x+
与x轴交于A(x1,0),B(x2,0)两点,且x1<x2,x12+x22=1.在y轴上,是否存在点P,使△ABP是直角三角形?若存在,求出点P及△ABP的面积;若不存在,请说明理由.
| 3 |
| 2 |
(1)若该函数的图象与x轴只有一个交点,求k的值;
(2)若点M(1,k)在某反比例函数的图象上,要使该反比例函数和二次函数y=kx2-2x+
| 3 |
| 2 |
(3)设抛物线y=kx2-2x+
| 3 |
| 2 |
分析:(1)本问注意分类讨论:若k=0,函数为一次函数;若k≠0,函数为二次函数,根据其△=0求解即可;
(2)根据反比例函数和二次函数的增减性,综合确定k应满足的条件和x的取值范围;
(3)由题意,首先根据一元二次方程根与系数关系,求出k的值;从而得到抛物线的解析式,画出抛物线的大致图象,以AB为直径作圆,圆与y轴的两个交点即为所求之点P;最后利用相似三角形求出点P的坐标和△ABP的面积.
(2)根据反比例函数和二次函数的增减性,综合确定k应满足的条件和x的取值范围;
(3)由题意,首先根据一元二次方程根与系数关系,求出k的值;从而得到抛物线的解析式,画出抛物线的大致图象,以AB为直径作圆,圆与y轴的两个交点即为所求之点P;最后利用相似三角形求出点P的坐标和△ABP的面积.
解答:解:(1)若k=0,则y=-2x+
是一次函数,与x轴只有一个交点,满足条件;
若k≠0,则y=kx2-2x+
(k≠0)是二次函数,
由△=b2-4ac=4-6k=0,得k=
.
∴k=0或
.
(2)设反比例函数解析式为:y=
,
∵点M(1,k)在反比例函数图象上,
∴m=k.
∴y=
.
由反比例函数的性质可知,当y随x的增大而增大时,须满足条件:k<0,x≠0.
二次函数y=kx2-2x+
,抛物线开口向下,其对称轴为直线x=
,
当y随x的增大而增大时,须满足条件:k<0,x<
.
综上所述,要使该反比例函数和二次函数都是y随x的增大而增大,须满足条件:k<0,x<
.
(3)存在.
抛物线解析式为:y=kx2-2x+
,
令y=0,即kx2-2x+
=0,
∴x1+x2=
,x1x2=
.
∵x12+x22=1,
∴(x1+x2)2-2x1x2=1,即:(
)2-2•
=1
整理得:k2+3k-4=0,
解得:k=-4或k=1.
又∵抛物线与x轴有两个交点,
∴△=4-6k>0,解得k<
,
∴k=1不符合题意,舍去,∴k=-4.
∴抛物线的解析式为:y=-4x2-2x+
=-4(x+
)2+
.
令y=0,解得x=
,
∴A(
,0),B(
,0).
画出函数大致图象如下,则OA=
,OB=
,AB=
.
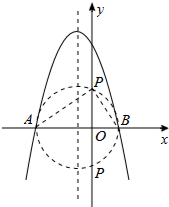
以AB为直径作圆,由图象可见,圆与y轴的交点有2个,因此所求的点P有两个.
连接PA、PB,易证△PAO∽△BPO,
∴
=
,
∴OP2=OA•OB=
×
=
,∴OP=
.
S△ABP=
AB•OP=
×
×
=
.
综上所述,存在两个满足条件的点P.点P的坐标为(0,
)或(0,-
),△ABP的面积为
.
| 3 |
| 2 |
若k≠0,则y=kx2-2x+
| 3 |
| 2 |
由△=b2-4ac=4-6k=0,得k=
| 2 |
| 3 |
∴k=0或
| 2 |
| 3 |
(2)设反比例函数解析式为:y=
| m |
| x |
∵点M(1,k)在反比例函数图象上,
∴m=k.
∴y=
| k |
| x |
由反比例函数的性质可知,当y随x的增大而增大时,须满足条件:k<0,x≠0.
二次函数y=kx2-2x+
| 3 |
| 2 |
| 1 |
| k |
当y随x的增大而增大时,须满足条件:k<0,x<
| 1 |
| k |
综上所述,要使该反比例函数和二次函数都是y随x的增大而增大,须满足条件:k<0,x<
| 1 |
| k |
(3)存在.
抛物线解析式为:y=kx2-2x+
| 3 |
| 2 |
令y=0,即kx2-2x+
| 3 |
| 2 |
∴x1+x2=
| 2 |
| k |
| 3 |
| 2k |
∵x12+x22=1,
∴(x1+x2)2-2x1x2=1,即:(
| 2 |
| k |
| 3 |
| 2k |
整理得:k2+3k-4=0,
解得:k=-4或k=1.
又∵抛物线与x轴有两个交点,
∴△=4-6k>0,解得k<
| 2 |
| 3 |
∴k=1不符合题意,舍去,∴k=-4.
∴抛物线的解析式为:y=-4x2-2x+
| 3 |
| 2 |
| 1 |
| 4 |
| 7 |
| 4 |
令y=0,解得x=
-1±
| ||
| 4 |
∴A(
-1-
| ||
| 4 |
-1+
| ||
| 4 |
画出函数大致图象如下,则OA=
1+
| ||
| 4 |
-1+
| ||
| 4 |
| ||
| 2 |

以AB为直径作圆,由图象可见,圆与y轴的交点有2个,因此所求的点P有两个.
连接PA、PB,易证△PAO∽△BPO,
∴
| OP |
| OB |
| OA |
| OP |
∴OP2=OA•OB=
1+
| ||
| 4 |
-1+
| ||
| 4 |
| 3 |
| 8 |
| ||
| 4 |
S△ABP=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
| ||
| 16 |
综上所述,存在两个满足条件的点P.点P的坐标为(0,
| ||
| 4 |
| ||
| 4 |
| ||
| 16 |
点评:本题是二次函数综合题型,考查了二次函数的图象与性质、反比例函数、一元二次方程、根与系数关系、根的判别式、相似三角形等知识点,有一定的难度.第(1)问中,须分一次函数、二次函数进行讨论;第(3)问中,满足条件的点P有两个,容易漏解.可见分类讨论思想是本题考查重点,也是易失分点.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
 (2013•怀化)如图,已知等腰梯形ABCD的底角∠B=45°,高AE=1,上底AD=1,则其面积为( )
(2013•怀化)如图,已知等腰梯形ABCD的底角∠B=45°,高AE=1,上底AD=1,则其面积为( ) (2013•怀化)如图,已知直线a∥b,∠1=35°,则∠2=
(2013•怀化)如图,已知直线a∥b,∠1=35°,则∠2= (2013•怀化)如图,已知在△ABC与△DEF中,∠C=54°,∠A=47°,∠F=54°,∠E=79°,求证:△ABC∽△DEF.
(2013•怀化)如图,已知在△ABC与△DEF中,∠C=54°,∠A=47°,∠F=54°,∠E=79°,求证:△ABC∽△DEF.