题目内容
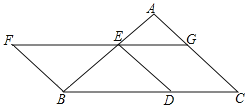
【题目】如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F,BD交AE于M. 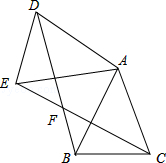
(1)求证:△AEC≌△ADB;
(2)若BC=2,∠BAC=30°,当四边形ADFC是菱形时,求BF的长.
【答案】
(1)解:由旋转的性质得:△ABC≌△ADE,且AB=AC,
∴AE=AD,AC=AB,∠BAC=∠DAE,
∴∠BAC+∠BAE=∠DAE+∠BAE,
即∠CAE=∠DAB,
在△AEC和△ADB中,
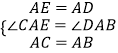 ,
,
∴△AEC≌△ADB(SAS)
(2)解:如图,过点B作BG⊥EC于点G,
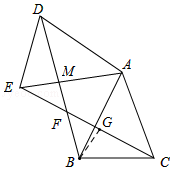
∵∠BAC=30°,AB=AC,
∴∠ABC=∠ACB=75°.
∵当四边形ADFC是菱形时,AC∥DF,
∴∠FBA=∠BAC=30°,
∵AB=AD,
∴∠ADB=∠ABD=30°,
∴∠ACE=∠ADB=30°,
∴∠FCB=45°.
∵BG⊥EC,
∴∠GBC=45°,
∴BG=GC=BCsin45°= ![]() ×2=
×2= ![]() ,
,
∵∠ABC=75°,∠ABD=30°,∠FCB=45°
∴∠BFC=180°﹣75°﹣45°﹣30°=30°,
∴BF=2BG=2 ![]()
【解析】(1)根据旋转的性质得:△ABC≌△ADE,且AB=AC,进而得到∠CAE=∠DAB,再根据SAS即可判定△AEC≌△ADB;(2)过点B作BG⊥EC于点G,根据四边形ADFC是菱形,以及等腰三角形的性质,得出∠FCB=45°,求得BG=GC=BCsin45°= ![]() ×2=
×2= ![]() ,再根据∠BFC=30°,即可得到BF=2BG.
,再根据∠BFC=30°,即可得到BF=2BG.
【考点精析】利用等腰直角三角形和含30度角的直角三角形对题目进行判断即可得到答案,需要熟知等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.

 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案【题目】某区在实施居民用水额定管理前,对居民生活用水情况进行了调查,下表是通过简单随机抽样获得的50个家庭去年月平均用水量(单位:吨),并将调查数据进行如下整理:
4.7 2.1 3.1 2.3 5.2 2.8 7.3 4.3 4.8 6.7
4.5 5.1 6.5 8.9 2.2 4.5 3.2 3.2 4.5 3.5
3.5 3.5 3.6 4.9 3.7 3.8 5.6 5.5 5.9 6.2
5.7 3.9 4.0 4.0 7.0 3.7 9.5 4.2 6.4 3.5
4.5 4.5 4.6 5.4 5.6 6.6 5.8 4.5 6.2 7.5
频数分布表
分组 | 划记 | 频数 |
2.0<x≤3.5 | 正正 | 11 |
3.5<x≤5.0 |
| 19 |
5.0<x≤6.5 | ||
6.5<x≤8.0 | ||
8.0<x≤9.5 |
| 2 |
合计 | 50 |
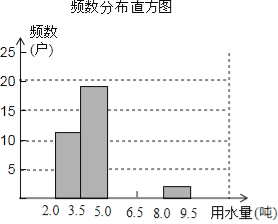
(1)把上面频数分布表和频数分布直方图补充完整;
(2)从直方图中你能得到什么信息?(写出两条即可);
(3)为了鼓励节约用水,要确定一个用水量的标准,超出这个标准的部分按1.5倍价格收费,若要使60%的家庭收费不受影响,你觉得家庭月均用水量应该定为多少?为什么?