题目内容
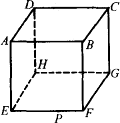
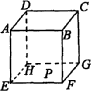
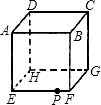如图是一个棱长为60cm的立方体ABCD-EFGH，一只小虫在棱EF上且距F点10cm的P处，它要爬到C点，则需要爬行的最短距离是（ ）| A、130 | ||
B、10
| ||
C、10
| ||
| D、不确定 |
分析：要求正方体中两点之间的最短路径，最直接的作法，就是将正方体展开，然后利用两点之间线段最短解答．
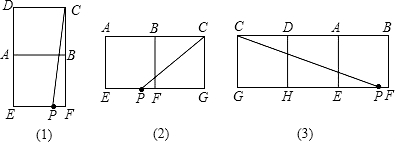
解答：解：展开后可分三种情况，
（1）CP=
=
=
=10
；
（2）CP=
=
=
=10
；
（3）CP=
=
=10
=50
．
综上所述，最短路径应为（2）所示，CP=10
．
故选B．
（1）CP=
| CF2+PF2 |
| 1202+102 |
| 14500 |
| 145 |
（2）CP=
| PG2+CG2 |
| 602+702 |
| 8500 |
| 85 |
（3）CP=
| PG2+CG2 |
| 602+1702 |
| 325 |
| 13 |
综上所述，最短路径应为（2）所示，CP=10
| 85 |
故选B．
点评：解答此题要注意以下几点：
（1）将立体图形展开的能力；
（2）分类讨论思想的应用；
（3）正确运用勾股定理．
（1）将立体图形展开的能力；
（2）分类讨论思想的应用；
（3）正确运用勾股定理．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
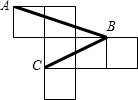
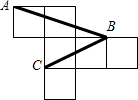如图为一个棱长为1的正方体的展开图，A、B、C是展开后小正方形的顶点，则∠ABC的度数为（ ）| A、30° | B、45° | C、50° | D、60° |
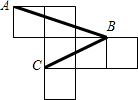如图为一个棱长为1的正方体的展开图，A、B、C是展开后小正方形的顶点，则∠ABC的度数为