题目内容
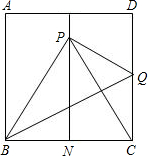 如图,有一块面积为4的正方形ABCD,M、N分别为AD、BC边上的中点,将C点折至MN上,落在P点位置,折痕为BQ,连接PQ、PC.
如图,有一块面积为4的正方形ABCD,M、N分别为AD、BC边上的中点,将C点折至MN上,落在P点位置,折痕为BQ,连接PQ、PC.
(1)试判断△PBC的形状,并说明理由;
(2)求PM的长.
解:(1)△PBC是正三角形,
理由:∵正方形ABCD中,AD BC,
BC,
而 ,∴AM
,∴AM BN,
BN,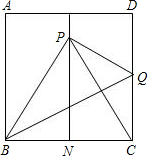
∴四边形ABNM是平行四边形,
∵∠A=90°,∴四边形ABNM是矩形,∴∠1=90°.
∵BN=NC,∴PB=PC,又由折叠知△BQC≌△BQP,
∴BP=BC,∴BP=PC=CB,∴△BPC是正三角形.
(2)由(1)得∠1=90°.∴∠4=90°.
∵S正方形ABCD=4,∴BC=AB=2,
由(1)及△PBC是正三角形,
∴PC=BC=2,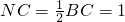 ,∴
,∴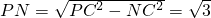 .
.
由(1)及矩形ABNM中,MN=AB=2,∴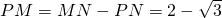 .
.
分析:由BN=CN,且MN⊥BC,可得PB=PC,再利用由折叠知△BQC≌△BQP,可得三条边相等,即为等边三角形.
求线段的长,利用勾股定理求解直角三角形即可.
点评:熟练掌握正方形的性质及等边三角形的判定,能够运用勾股定理求解一些简单的计算问题.
理由:∵正方形ABCD中,AD
 BC,
BC,而
 ,∴AM
,∴AM BN,
BN,
∴四边形ABNM是平行四边形,
∵∠A=90°,∴四边形ABNM是矩形,∴∠1=90°.
∵BN=NC,∴PB=PC,又由折叠知△BQC≌△BQP,
∴BP=BC,∴BP=PC=CB,∴△BPC是正三角形.
(2)由(1)得∠1=90°.∴∠4=90°.
∵S正方形ABCD=4,∴BC=AB=2,
由(1)及△PBC是正三角形,
∴PC=BC=2,
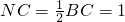 ,∴
,∴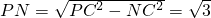 .
.由(1)及矩形ABNM中,MN=AB=2,∴
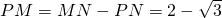 .
.分析:由BN=CN,且MN⊥BC,可得PB=PC,再利用由折叠知△BQC≌△BQP,可得三条边相等,即为等边三角形.
求线段的长,利用勾股定理求解直角三角形即可.
点评:熟练掌握正方形的性质及等边三角形的判定,能够运用勾股定理求解一些简单的计算问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
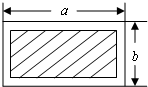 25、如图,有一块长为a米、宽为b米的长方形空地,现计划将这块空地四周均留出2米宽修道路,中间用来绿化.
25、如图,有一块长为a米、宽为b米的长方形空地,现计划将这块空地四周均留出2米宽修道路,中间用来绿化.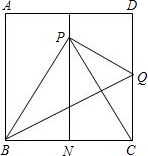 如图,有一块面积为4的正方形ABCD,M、N分别为AD、BC边上的中点,将C点折至MN上,落在P点位置,折痕为BQ,连接PQ、PC.
如图,有一块面积为4的正方形ABCD,M、N分别为AD、BC边上的中点,将C点折至MN上,落在P点位置,折痕为BQ,连接PQ、PC. 如图,有一块长为40米,宽为30米的长方形绿地.其中有两条互相垂直的笔直的道路(图中的阴影部分),道路的一边GF与长方形绿地一边的夹角为60°,且道路的出入口的边AB、CD、EF、GH的长度都相同,已知道路面积为137平方米,求道路出入口的边的长度.
如图,有一块长为40米,宽为30米的长方形绿地.其中有两条互相垂直的笔直的道路(图中的阴影部分),道路的一边GF与长方形绿地一边的夹角为60°,且道路的出入口的边AB、CD、EF、GH的长度都相同,已知道路面积为137平方米,求道路出入口的边的长度. 如图,有一块长为40米,宽为30米的长方形绿地.其中有两条互相垂直的笔直的道路(图中的阴影部分),道路的一边GF与长方形绿地一边的夹角为60°,且道路的出入口的边AB、CD、EF、GH的长度都相同,已知道路面积为137平方米,求道路出入口的边的长度.
如图,有一块长为40米,宽为30米的长方形绿地.其中有两条互相垂直的笔直的道路(图中的阴影部分),道路的一边GF与长方形绿地一边的夹角为60°,且道路的出入口的边AB、CD、EF、GH的长度都相同,已知道路面积为137平方米,求道路出入口的边的长度.