题目内容
如图,点O是边为2的正方形ABCD的中心,点E从A点开始沿AD边运动,点F从D点开始沿DC边运动,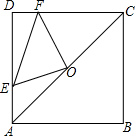 并且AE=DF.
并且AE=DF.(1)求正方形ABCD的对角线AC的长;
(2)若点E、F同时运动,连接OE、OF,请你探究:四边形DEOF的面积S与正方形ABCD的面积关系,并求出四边形DEOF的面积S;
(3)在(2)的基础上,设AE=x,△EOF的面积为y,y与x之间的函数关系式,写出自变量x的取值范围,并利用图象说明当x在什么范围时,y≥
| 5 | 8 |
分析:(1)可根据勾股定理得出AC的长.
(2)连接OD,先证△AEO≌△DFO,然后得出S△OFD=S△AEO,因此四边形DEOF的面积就转化为三角形AOD的面积.三角形AOD的面积是正方形的
,由此可求出S的值.
(3)由(2)得出的四边形BEOF的面积,那么y=1-S△DEF=然后用x表示出三角形DEF的面积,即可得出函数式.
(2)连接OD,先证△AEO≌△DFO,然后得出S△OFD=S△AEO,因此四边形DEOF的面积就转化为三角形AOD的面积.三角形AOD的面积是正方形的
| 1 |
| 4 |
(3)由(2)得出的四边形BEOF的面积,那么y=1-S△DEF=然后用x表示出三角形DEF的面积,即可得出函数式.
解答: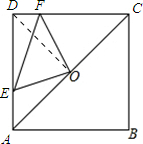 解:(1)在直角三角形ABC中
解:(1)在直角三角形ABC中
AC=
=2
.
(2)连接OD,
∵OA=OD,AE=DF,∠ODC=∠OAD=45°
∴△AEO≌△DFO
∴S△OFD=S△AEO则S四边形DEOF=S△ADO
又S△ADO=
S四边形ABCD,
∴S四边形DEOF=
S四边形ABCD=1.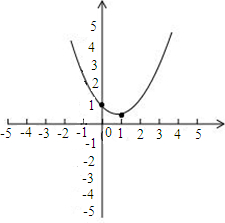
(3)由(2)得:y=1-S△DEF=1-
x(2-x)=
x2-x+1
且0≤x≤2
配方得:y=
(x-1)2+
画图:
令y=
时,
(x-1)2+
=
∴x1=
,x2=
由图象可知:当0≤x≤
时,或
≤x≤2时y≥
.
 解:(1)在直角三角形ABC中
解:(1)在直角三角形ABC中AC=
| AB2+BC2 |
| 2 |
(2)连接OD,
∵OA=OD,AE=DF,∠ODC=∠OAD=45°
∴△AEO≌△DFO
∴S△OFD=S△AEO则S四边形DEOF=S△ADO
又S△ADO=
| 1 |
| 4 |
∴S四边形DEOF=
| 1 |
| 4 |
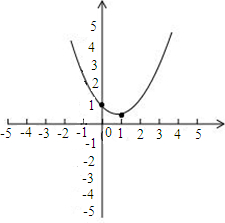
(3)由(2)得:y=1-S△DEF=1-
| 1 |
| 2 |
| 1 |
| 2 |
且0≤x≤2
配方得:y=
| 1 |
| 2 |
| 1 |
| 2 |
画图:
令y=
| 5 |
| 8 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 8 |
∴x1=
| 1 |
| 2 |
| 3 |
| 2 |
由图象可知:当0≤x≤
| 1 |
| 2 |
| 3 |
| 2 |
| 5 |
| 8 |
点评:本题主要考查了正方形的性质和二次函数的综合应用,本题中利用全等三角形来转化面积是解题的关键.

练习册系列答案
相关题目
 (2013•本溪)如图,点B1是面积为1的等边△OBA的两条中线的交点,以OB1为一边,构造等边△OB1A1(点O,B1,A1按逆时针方向排列),称为第一次构造;点B2是△OB1A1的两条中线的交点,再以OB2为一边,构造等边△OB2A2(点O,B2,A2按逆时针方向排列),称为第二次构造;以此类推,当第n次构造出的等边△OBnAn的边OAn与等边△OBA的边OB第一次重合时,构造停止.则构造出的最后一个三角形的面积是
(2013•本溪)如图,点B1是面积为1的等边△OBA的两条中线的交点,以OB1为一边,构造等边△OB1A1(点O,B1,A1按逆时针方向排列),称为第一次构造;点B2是△OB1A1的两条中线的交点,再以OB2为一边,构造等边△OB2A2(点O,B2,A2按逆时针方向排列),称为第二次构造;以此类推,当第n次构造出的等边△OBnAn的边OAn与等边△OBA的边OB第一次重合时,构造停止.则构造出的最后一个三角形的面积是
 并且AE=DF.
并且AE=DF. .
. .
.