题目内容
设sinα、cosα是方程x2-
x+
=0的两根,△ABC的三边分别为sinα、cosα、
m,则△ABC的形状是______三角形.
| m |
| 1 |
| 2 |
| 1 |
| 2 |
∵sinα、cosα是方程x2-
x+
=0的两根,
∴sinα+cosα=
①,sinα•cosα=
②,sin2α+cos2α=1③,
①式两边平方得,sin2α+cos2α+2sinα•cosα=m④,
把②③代入④得,1+1=m,
∴m=2,
∴△ABC的三边分别为sinα,cosα,1,
而sin2α+cos2α=12,
∴△ABC为直角三角形.
故答案为:直角.
| m |
| 1 |
| 2 |
∴sinα+cosα=
| m |
| 1 |
| 2 |
①式两边平方得,sin2α+cos2α+2sinα•cosα=m④,
把②③代入④得,1+1=m,
∴m=2,
∴△ABC的三边分别为sinα,cosα,1,
而sin2α+cos2α=12,
∴△ABC为直角三角形.
故答案为:直角.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
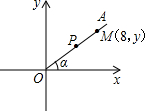 如图,以O为端点的射线OA所在直线的函数关系式为y=
如图,以O为端点的射线OA所在直线的函数关系式为y=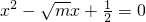 的两根,△ABC的三边分别为
的两根,△ABC的三边分别为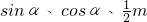 ,则△ABC的形状是________三角形.
,则△ABC的形状是________三角形.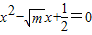 的两根,△ABC的三边分别为
的两根,△ABC的三边分别为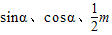 ,则△ABC的形状是 三角形.
,则△ABC的形状是 三角形.