��Ŀ����
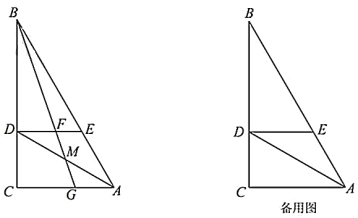
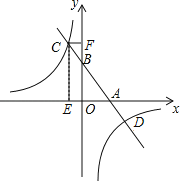
����Ŀ����ͼ1����֪������y1��x2+mx��������y2��ax2+bx+c����״��ͬ�����ڷ����෴�����ཻ�ڵ�A����3����6���͵�B��1��6����������y2��x�������ύ�ڵ�C��PΪ������y2��A��B�����һ���㣬����P��PQ��y�ᣬ��y1���ڵ�Q��
��1����������y1��������y2�Ľ���ʽ��
��2���ı���APBO�����ΪS����S�����ֵ����д����ʱ��P�����ꣻ
��3����ͼ2��y2�ĶԳ���Ϊֱ��l��PC��l���ڵ�E���ڣ�2���������£�ֱ��l���Ƿ����һ��T��ʹ����T��E��CΪ���������������APQ���ƣ�������ڣ������T�����ꣻ��������ڣ�˵�����ɣ�

���𰸡���1��y2����x2+x+6����2����t����1ʱ��S�����16����ʱP������Ϊ����1��4������3�����ڵ�T������![]() ��
��![]() ʹ��T��C��EΪ��������������PAQ���ƣ�
ʹ��T��C��EΪ��������������PAQ���ƣ�
��������
��1���ֱ����ô���ϵ�������������κ����Ľ���ʽ��
��2�����P������Ϊt����P��t����t2+t+6����Q��t��t2+5t������ʾPQ�ij�������������������Ϳɵ�S��t�Ĺ�ϵʽ���䷽��ɵ�S�����ֵ��
��3����ȷ����AQB��135�������Է�������ۿɵý��ۣ�
�⣺��1����B��1��6������y1��x2+mx�ã�m��5��
��y1��x2+5x��
��y2��y1��״��ͬ�������෴��
��a����1��
��y2����x2+bx+c��
��A����3����6����B��1��6������ã�
![]() ��
��
��ã�b��1��c��6��
��y2����x2+x+6��
��2�����P������Ϊt��
��P��t����t2+t+6����Q��t��t2+5t����
��PQ����t2+t+6��t2��5t����2t2��4t+6��
��S�ı���APBQ��![]()
����4��t+1��2+16��
�൱t����1ʱ��S�����16����ʱP������Ϊ����1��4����
��3�����ڵ�T��
��y2����x2+x+6����ֱ��lΪ��x��![]() ��
��
�ɣ�2��֪P�������Ϊ����1��4����
��x����1ʱ��y1������1��2+5������1������4��
��Q�����������1����4����
��A����3����6����
�x2+x+6��0�ã�CΪ��3��0����
��ͼ2����PQ��x�ύ�ڵ�G��ֱ��l��x�ύ�ڵ�M��

��AH��PQ���ӳ��ߣ�����Ϊ��H����֪AH��2��HQ����4������6����2��
���AQH��45����
���AQP��180����45����135����
��PG��4��CG��3+1��4��
���ECO��45����
��T����E���Ϸ���CET��135��
MC��3��![]() ��
��![]() ��EC��
��EC��![]() MC��
MC��![]() ��
��
AQ��![]() AH��2
AH��2![]() ��PQ��8��
��PQ��8��
�������������
������PAQ�ס�TCE����![]() ��
��
��TE��![]() ��10����ʱT������Ϊ
��10����ʱT������Ϊ![]() ��
��
������PAQ�ס�CTE����![]() ��
��
��TE��![]() ����ʱT������Ϊ
����ʱT������Ϊ![]() ,
,
���Ͽ�֪���ڵ�T������![]() ��
��![]() ʹ��T��C��EΪ���������������PAQ���ƣ�
ʹ��T��C��EΪ���������������PAQ���ƣ�

 ��ĩ1�����ʽ���������ϵ�д�
��ĩ1�����ʽ���������ϵ�д�����Ŀ������һ����ͯ�ڣ�ij��߳���������һ����ͼ��ʾ�Ŀ�������ת����ת�̣���չ�н��������˿�����߾��ܻ��һ��ת��ת�̵Ļ��ᣬ��ת��ֹͣʱ��ָ��������һ����Ϳ��Ի����Ӧ��Ʒ���±��Ǹû��һ��ͳ�����ݣ�����˵�����ٵ�n�ܴ�ʱ������ָ��������Ǧ���������Ƶ�ʴ�Լ��0.70���ڼ�����ȥת��ת��һ�Σ����Ǧ�ʵĸ��ʴ�Լ��0.70�������ת��ת��2000�Σ�ָ���������ľߺ�������Ĵ�����Լ��600�Σ���ת��ת��10�Σ�һ����3�λ���ľߺ�.����ȷ����_____
ת��ת�̵Ĵ���n | 100 | 150 | 200 | 500 | 800 | 1000 |
������Ǧ��������Ĵ���m | 68 | 108 | 140 | 355 | 560 | 690 |
������Ǧ���������Ƶ�� | 0.68 | 0.72 | 0.70 | 0.71 | 0.70 | 0.69 |