题目内容
24、(1)例:代数式(a+b)2表示a、b两数和的平方.仿照上例填空:
代数式a2-b2表示
代数式(a+b)(a-b)表示
(2)试计算a、b取不同数值时,a2-b2及(a+b)(a-b)的植,填入下表:

(3)请你再任意给a、b各取一个数值,并计算a2-b2及(a+b)(a-b)的植:
当a=
(4)我的发现:
(5)用你发现的规律计算:78.352-21.652
代数式a2-b2表示
a、b两数平方的差
.代数式(a+b)(a-b)表示
a、b两数的和与两数的差的积
.(2)试计算a、b取不同数值时,a2-b2及(a+b)(a-b)的植,填入下表:

(3)请你再任意给a、b各取一个数值,并计算a2-b2及(a+b)(a-b)的植:
当a=
2
,b=1
时,a2-b2=3
,(a+b)(a-b)=3
.(4)我的发现:
a2-b2=(a+b)(a-b)
.(5)用你发现的规律计算:78.352-21.652
分析:(1)根据两式的意义即可写出;
(2)分别代入求值即可;
(3)任意给a、b各取一个数值,代入求值,即可;
(4)根据前边的计算,总结出a2-b2与(a+b)(a-b)的大小关系即可;
(5)利用(4)中的关系,计算即可.
(2)分别代入求值即可;
(3)任意给a、b各取一个数值,代入求值,即可;
(4)根据前边的计算,总结出a2-b2与(a+b)(a-b)的大小关系即可;
(5)利用(4)中的关系,计算即可.
解答:解:(1)a、b两数平方的差;a、b两数的和与两数的差的积(2分)
(2)(3分)
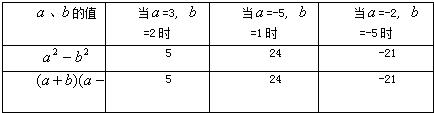
(3)a=2,b=1时,a2-b2=3,(a+b)(a-b)=3
(4)a2-b2=(a+b)(a-b)(2分)
(5)78.352-21.652=(78.35+21.65)(78.35-21.65)=5670(3分)
(2)(3分)

(3)a=2,b=1时,a2-b2=3,(a+b)(a-b)=3
(4)a2-b2=(a+b)(a-b)(2分)
(5)78.352-21.652=(78.35+21.65)(78.35-21.65)=5670(3分)
点评:本题主要是通过实例探究了平方差公式,正确理解题目每部提出的要求是解决本题的关键.

练习册系列答案
相关题目



