题目内容
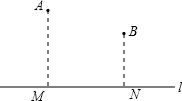
在一平直河岸l同侧有A,B两个村庄,A,B到l的距离分别是3km和2km,AB=akm(a>1).现计划在河岸l上建一抽水站P,用输水管向两个村庄供水.方案设计:
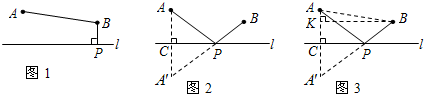
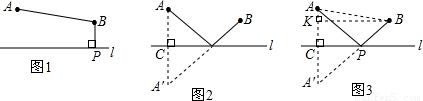
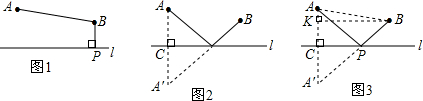
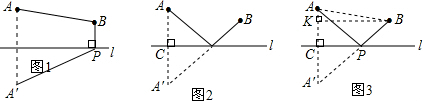
某班数学兴趣小组设计了两种铺设管道方案:图1是方案一的示意图,设该方案中管道长度为d1,且d1=PB+BA(km)(其中BP⊥l于点p);图2是方案二的示意图,设该方案中管道长度为d2,且d2=PA+PB(km)(其中点A'与点A关于I对称,A′B与l交于点P.
观察计算:
(1)在方案一中,d1=
(2)在方案二中,组长小宇为了计算d2的长,作了如图3所示的辅助线,请你按小宇同学的思路计算,
d2=

探索归纳
(1)①当a=4时,比较大小:d1(
②当a=6时,比较大小:d1(
(2)请你参考右边方框中的方法指导,就a(当a>1时)的所有取值情况进行分析,要使铺设的管道长度较短,应选择方案一还是方案二?
分析:运用勾股定理和轴对称求出d2,根据方法指导,先求d12-d22,再根据差进行分类讨论选取合理方案.
解答:解:(1)∵A和A'关于直线l对称,
∴PA=PA',
d1=PB+BA=PB+PA'=a+2;
故答案为:a+2;
(2)因为BK2=a2-1,
A'B2=BK2+A'K2=a2-1+52=a2+24
所以d2=
.
探索归纳:
(1)①当a=4时,d1=6,d2=
,d1<d2;
②当a=6时,d1=8,d2=
,d1>d2;
(2)d12-d22=(a+2)2-(
)2=4a-20.
①当4a-20>0,即a>5时,d12-d22>0,
∴d1-d2>0,
∴d1>d2;
②当4a-20=0,即a=5时,d12-d22=0,
∴d1-d2=0,
∴d1=d2
③当4a-20<0,即a<5时,d12-d22<0,
∴d1-d2<0,
∴d1<d2
综上可知:当a>5时,选方案二;
当a=5时,选方案一或方案二;
当1<a<5(缺a>1不扣分)时,选方案一.

∴PA=PA',
d1=PB+BA=PB+PA'=a+2;
故答案为:a+2;
(2)因为BK2=a2-1,
A'B2=BK2+A'K2=a2-1+52=a2+24
所以d2=
| a2+24 |
探索归纳:
(1)①当a=4时,d1=6,d2=
| 40 |
②当a=6时,d1=8,d2=
| 60 |
(2)d12-d22=(a+2)2-(
| a2+24 |
①当4a-20>0,即a>5时,d12-d22>0,
∴d1-d2>0,
∴d1>d2;
②当4a-20=0,即a=5时,d12-d22=0,
∴d1-d2=0,
∴d1=d2
③当4a-20<0,即a<5时,d12-d22<0,
∴d1-d2<0,
∴d1<d2
综上可知:当a>5时,选方案二;
当a=5时,选方案一或方案二;
当1<a<5(缺a>1不扣分)时,选方案一.
点评:本题为方案设计题,综合考查了学生的作图能力,运用数学知识解决实际问题的能力,以及观察探究和分类讨论的数学思想方法.

练习册系列答案
相关题目