题目内容
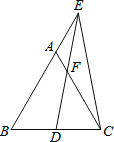
【题目】如图,在等边△ABC中,点D是BC中点,点E在BA的延长线上,ED=EC,AC和ED交于点F,若AE=![]() ,则CF= .
,则CF= .
【答案】![]()
【解析】
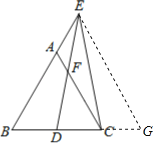
试题分析:作EG∥AC交BC的延长线于G,根据平行线的性质和等边三角形的性质得到△EBG是等边三角形,求出CG的长,证明△BED≌△GEC,求出BD,根据三角形中位线定理计算即可.
解:作EG∥AC交BC的延长线于G,
∵△ABC是等边三角形,
∴∠ACB=60°,
∴∠G=60°,又∠B=60°,
∴△EBG是等边三角形,
∴EB=EG=BG,
∴CG=AE=![]() ,
,
∵ED=EC,
∴∠EDC=∠ECD,又∠B=∠G,
∴∠BED=∠GEC,
在△BED和△GEC中,
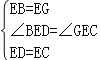 ,
,
∴△BED≌△GEC,
∴BD=CG=![]() ,
,
∴EG=BG=![]() ,
,
∵EG∥AC,DC=CG,
∴CF=![]() EG=
EG=![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目