题目内容
已知矩形ABCD中,AB=4,BC=8,E是DC上一点,连AE并延长交BC的延长线于点F,正方形CGHM的顶点G、H、M分别在△ECF的三边上.(1)当点E为DC中点时,求正方形CGHM的边长a1;
(2)当DE=
| 1 |
| 3 |
(3)当DE=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n+1 |
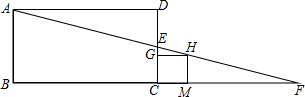 形CGHM的边长分别记为a1、a2、a3、…、an,则an=
形CGHM的边长分别记为a1、a2、a3、…、an,则an=分析:易得△HGE∽△ADE,有GH:AD=GE:DE,EG=CD-GH-DE,故可求得GH.
解答:解:∵GH∥AD,
∴△HGE∽△ADE.
∴GH:AD=GE:DE.
把EG=CD-GH-DE,CD=4,AD=8,DE=
DC代入上式,解得,GH=
.
∴(1)当n=1时,有a1=GH=
;
∴(2)当n=2时,有a2=GH=
;
∴(3)an=GH=
.
∴△HGE∽△ADE.
∴GH:AD=GE:DE.
把EG=CD-GH-DE,CD=4,AD=8,DE=
| 1 |
| n+1 |
| 8n |
| 2n+3 |
∴(1)当n=1时,有a1=GH=
| 8 |
| 5 |
∴(2)当n=2时,有a2=GH=
| 16 |
| 7 |
∴(3)an=GH=
| 8n |
| 2n+3 |
点评:本题利用了正方形的性质,平行线的性质,相似三角形的判定和性质求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,点Q从点B以每秒1个单位沿BA方向向点A运动,设运动时间为t秒,△BPQ的面积为S.
,点Q从点B以每秒1个单位沿BA方向向点A运动,设运动时间为t秒,△BPQ的面积为S. 如图,已知矩形ABCD中,BC=6,AB=8,延长AD到点E,使AE=15,连接BE交AC于点P.
如图,已知矩形ABCD中,BC=6,AB=8,延长AD到点E,使AE=15,连接BE交AC于点P. 如图:已知矩形ABCD中,CE∥DF.
如图:已知矩形ABCD中,CE∥DF.