题目内容
30、如图1,已知直线m∥n,点A、B在直线n上,点C、P在直线m上:
(1)请写出图1中所有的面积相等的各对三角形:
(2)如图1,不难证明,点P在直线m上移动到任一位置时,总有△ABP与△ABC的面积相等;如图2,点M在△ABC的边上,请过点M画一条直线,平分△ABC的面积.(保留作图痕迹,并对作法做简要说明)
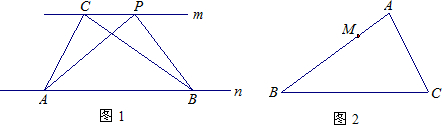
(1)请写出图1中所有的面积相等的各对三角形:
△ABC和△BPA(或△PCA和△CPB或△ACO和△POB)
;(2)如图1,不难证明,点P在直线m上移动到任一位置时,总有△ABP与△ABC的面积相等;如图2,点M在△ABC的边上,请过点M画一条直线,平分△ABC的面积.(保留作图痕迹,并对作法做简要说明)
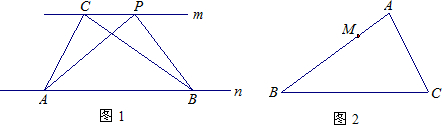
分析:(1)根据平行线间的距离相等和三角形的面积公式即可求解,
(2)作出AB的垂直平分线,利用CM是三角形的中线,交点即是M的位置,过点M画一条直线,即可平分△ABC的面积.
(2)作出AB的垂直平分线,利用CM是三角形的中线,交点即是M的位置,过点M画一条直线,即可平分△ABC的面积.
解答: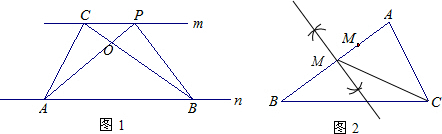 (1)解:∵m∥n,
(1)解:∵m∥n,
∴△ABC和△BPA的面积相等,△APC和△BPC的面积相等,
∴根据等式的性质,得△ACO和△POC的面积相等.
故答案为:△ABC和△BPA(或△PCA和△CPB或△ACO和△POB);
(2)如图所示,作出AB的垂直平分线,交点即是M的位置,
此时CM平分△ABC的面积.
 (1)解:∵m∥n,
(1)解:∵m∥n,∴△ABC和△BPA的面积相等,△APC和△BPC的面积相等,
∴根据等式的性质,得△ACO和△POC的面积相等.
故答案为:△ABC和△BPA(或△PCA和△CPB或△ACO和△POB);
(2)如图所示,作出AB的垂直平分线,交点即是M的位置,
此时CM平分△ABC的面积.
点评:此题考查了平行线的性质和三角形的面积相等的方法.等底等高的两个三角形的面积相等.

练习册系列答案
相关题目
 如图1,已知直线:
如图1,已知直线: