题目内容
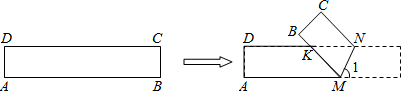
 如图,ABCD是一张长方形纸片,AD=BC=1,AB=CD=5.在边AB上取一点M,在CD上取一点N,将纸片沿MN折叠,
如图,ABCD是一张长方形纸片,AD=BC=1,AB=CD=5.在边AB上取一点M,在CD上取一点N,将纸片沿MN折叠,(1)当点B和点D重合时,若∠1=70°,则∠NDM的度数为
40°
40°
;(2)线段AM的长度为
2.4
2.4
.分析:(1)利用翻折变换的性质得出∠1=∠NMD,进而得出∠DMA的度数,即可得出∠NDM的度数;
(2)在Rt△ADM中,利用AD2+AM2=DM2,得出即可.
(2)在Rt△ADM中,利用AD2+AM2=DM2,得出即可.
解答:解:(1)∵将纸片沿MN折叠,点B和点D重合时,
∴∠1=∠NMD,
∵∠1=70°,
∴∠DMA=180°-70°-70°=40°,
∵CD∥AB
∴∠NDM=∠DMA,
∴∠NDM的度数为40°;
故答案为:40°;
(2)设AM=x,则DM=5-x,
在Rt△ADM中,
AD2+AM2=DM2,
∴12+x2=(5-x)2,
解得:x=2.4.
故答案为:2.4.
∴∠1=∠NMD,
∵∠1=70°,
∴∠DMA=180°-70°-70°=40°,
∵CD∥AB
∴∠NDM=∠DMA,
∴∠NDM的度数为40°;
故答案为:40°;
(2)设AM=x,则DM=5-x,
在Rt△ADM中,
AD2+AM2=DM2,
∴12+x2=(5-x)2,
解得:x=2.4.
故答案为:2.4.
点评:此题主要考查了翻折变换的性质和勾股定理等知识,根据已知设AM=x,则DM=5-x进而利用勾股定理得出是解题关键.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
 B、
B、 C、
C、 D、
D、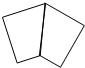
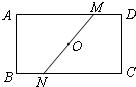
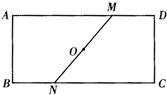 20、如图,ABCD是一张矩形纸片,点O为矩形对角线的交点,直线MN经过点O交AD于M,交BC于N.
20、如图,ABCD是一张矩形纸片,点O为矩形对角线的交点,直线MN经过点O交AD于M,交BC于N.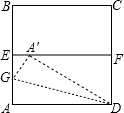 如图,ABCD是一张边长为4cm的正方形纸片,E,F分别为AB,CD的中点,沿过点D的折痕将A 角翻折,使得点A落在EF上的点A′处,折痕交AE于点G,则EG=
如图,ABCD是一张边长为4cm的正方形纸片,E,F分别为AB,CD的中点,沿过点D的折痕将A 角翻折,使得点A落在EF上的点A′处,折痕交AE于点G,则EG=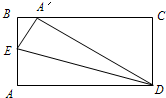 15、如图,ABCD是一张矩形纸片,沿过点D的折痕将A角翻折,使得点A落在BC上,折痕交AB于点E,若BC=2AB,则∠A′EB=
15、如图,ABCD是一张矩形纸片,沿过点D的折痕将A角翻折,使得点A落在BC上,折痕交AB于点E,若BC=2AB,则∠A′EB=