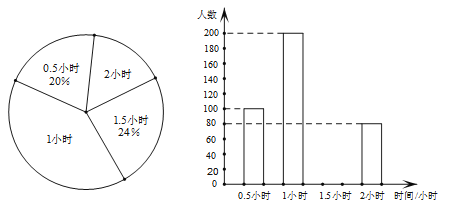
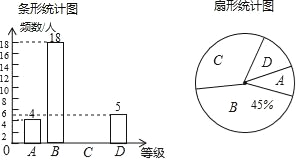
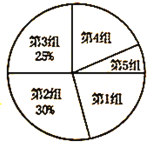
题目内容
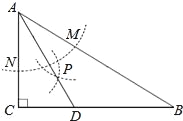
【题目】如图1,我们将相同的两块含30°角的直角三角板Rt△DEF与Rt△ABC叠合,使DE在AB上,DE过点C,已知AC=DE=6.
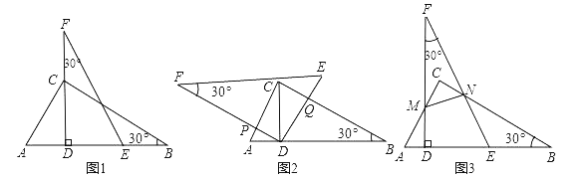
(1)将图1中的△DEF绕点D逆时针旋转(DF与AB不重合),使边DF、DE分别交AC、BC于点P、Q,如图2.
①求证:△CQD∽△APD;②连接PQ,设AP=x,求面积S△PCQ关于x的函数关系式;
(2)将图1中的△DEF向左平移(点A、D不重合),使边FD、FE分别交AC、BC于点M、N设AM=t,如图3.
①判断△BEN是什么三角形?并用含t的代数式表示边BE和BN;②连接MN,求面积S△MCN关于t的函数关系式;
(3)在旋转△DEF的过程中,试探求AC上是否存在点P,使得S△PCQ等于平移所得S△MCN的最大值?说明你的理由.
【答案】(1)①见解析;②![]() ;(2)①△BEN是等腰三角形,BE=6﹣
;(2)①△BEN是等腰三角形,BE=6﹣![]() t,BN=
t,BN=![]() (6﹣
(6﹣![]() t),②
t),②![]() ;(3)存在,见解析.
;(3)存在,见解析.
【解析】
(1)①易得∠BCD=∠A=60°,∠ADP=∠CDE,那么可得△CQD∽△APD②利用相似可得CQ=![]() x,那么PC=6﹣x.可表示出S△PCQ
x,那么PC=6﹣x.可表示出S△PCQ
(2)①由外角∠FEN=60°,∠B=30°,可得∠BNE=30°,∴NE=BN,那么△BEN是等腰三角形.易得AD=![]() t,AB=12,那么BE=12﹣AD﹣DE=6﹣
t,AB=12,那么BE=12﹣AD﹣DE=6﹣![]() t.过E作EG⊥BN于点G.利用30°的三角函数可求得BG,进而求得BN
t.过E作EG⊥BN于点G.利用30°的三角函数可求得BG,进而求得BN
②容易利用t表示出MC、CN,即可表示出所求面积
(3)利用二次函数的最值表示出S△MCN的最大值,让前面所求的面积的代数式等于即可.
(1)①证明:∵∠F=∠B=30°,∠ACB=∠BDF=90°∴∠BCD=∠A=60°,∵∠ADP+∠PDC=90°,∠CDE+∠PDC=90°∴△CQD∽△APD
②∵在Rt△ADC中,AD=3,DC=3![]()
又∵△CQD∽△APD,CQ=![]() x.
x.
∴![]()
(2)①△BEN是等腰三角形.BE=6﹣![]() t,BN=
t,BN=![]() (6﹣
(6﹣![]() t).
t).
②S△MCN=![]() (6﹣t)×
(6﹣t)×![]()
(3)存在.
由题意建立方程![]() ,
,
解得x=![]() 或
或![]()
即当AP=![]() 或AP=
或AP=![]() 时,S△PCQ等于S△MCN的最大值.
时,S△PCQ等于S△MCN的最大值.

 优生乐园系列答案
优生乐园系列答案