题目内容
【题目】一次函数y1=kx+b与y2=x+a的图象如图所示,则下列结论:①k<0;②a>0;③当x<3时,y1<y2;④当y1>0且y2>0时,﹣a<x<4.其中正确的个数是( )
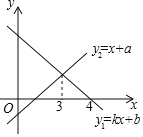
A. 1个B. 2个C. 3个D. 4个
【答案】B
【解析】
仔细观察图象,①k的正负看函数图象从左向右成何趋势即可;②a看y2=x+a与y轴的交点坐标;③以两条直线的交点为分界,哪个函数图象在上面,则哪个函数值大;④看两直线都在x轴上方的自变量的取值范围.
①∵y1=kx+b的图象从左向右呈下降趋势,
∴k<0正确;
②∵y2=x+a,与y轴的交点在负半轴上,
∴a<0,故②错误;
③当x<3时,y1>y2,故③错误;
④y2=x+a与x轴交点的横坐标为x=﹣a,
当y1>0且y2>0时,﹣a<x<4正确;
故正确的判断是①④,正确的个数是2个.
故选:B.

练习册系列答案
相关题目
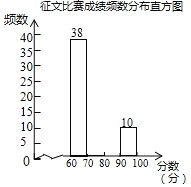
【题目】今年我区作为全国作文教学改革试验区,举办了中小学生现场作文大赛,全区七、八年级的学生参加了中学组的比赛,大赛组委会对参赛获奖作品的成绩进行统计,每篇获奖作品成绩为m分(60≤m≤100)绘制了如下两幅数据信息不完整的统计图表.
获奖作品成绩频数分布表
分数段 | 频数 | 频率 |
60≤x<70 | 38 | 0.38 |
70≤x<80 | a | 0.32 |
80≤x<90 | b | |
90≤x<100 | 10 | |
合计 | 1 |
请根据以上信息,解决下列问题:
(1)获奖作品成绩频数分布表中a= ,b= ;
(2)把获奖作品成绩频数分布直方图缺失的信息补全;
(3)某校八年级二班有两名男同学和两名女同学在这次大赛中获奖,并且其中两名同学获得了大赛一等奖,请用列表或画树状图法求出恰好一男一女获得一等奖的概率.