题目内容
【题目】作出函数y=﹣x+3的图象,并利用图象回答问题:
(1)当y<0时,x的取值范围为_____;
(2)当﹣2<x<2时,y的取值范围为_____;
(3)图象与直线y=x﹣1的交点坐标为______;这两条直线与y轴围成的三角形面积为______.

【答案】(1) x>3;(2) 1<y<5;(3)(2,1);4.
【解析】
(1)根据题意可知所求的是直线y=﹣x+3在x轴下方部分x的取值范围;
(2)根据题意可知所求的是直线y=﹣x+3在﹣2<x<2范围内y的取值范围;
(3)作出直线y=x﹣1,即可得到两直线的交点坐标,进而得到这两条直线与y轴围成的三角形面积.
解:y=﹣x+3,令x=0,则y=3;令y=0,则x=3;
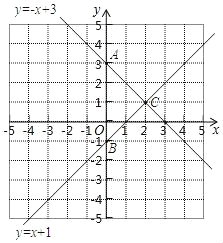
如图所示,直线y=﹣x+3即为所求;
(1)当y<0时,x的取值范围为x>3;
(2)当﹣2<x<2时,y的取值范围为1<y<5;
(3)如图,作出直线y=x﹣1,B点坐标为(0,-1),两直线的交点为C(2,1);
这两条直线与y轴围成的△ABC的面积为![]() ×4×2=4.
×4×2=4.
故答案为:x>3;1<y<5;(2,1);4.

练习册系列答案
相关题目