题目内容
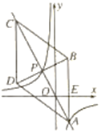
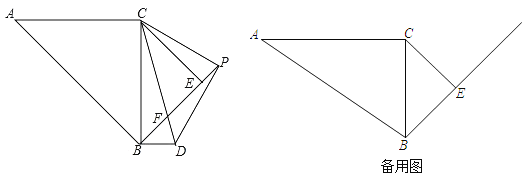
【题目】如图,在△ABC中,∠ACB=90°,tanA=![]() ,AC=6
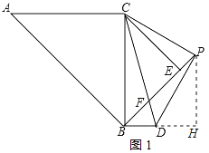
,AC=6![]() ,以BC为斜边向右侧作等腰直角△EBC,P是BE延长线上一点,连接PC,以PC为直角边向下方作等腰直角△PCD,CD交线段BE于点F,连接BD.
,以BC为斜边向右侧作等腰直角△EBC,P是BE延长线上一点,连接PC,以PC为直角边向下方作等腰直角△PCD,CD交线段BE于点F,连接BD.
(1)求证:PC:CD=CE:BC;
(2)若PE=n(0<n≤4),求△BDP的面积;(用含n的代数式表示)
(3)当△BDF为等腰三角形时,请直接写出线段PE的长度.
【答案】(1)证明见解析;(2)S=2n2+![]() n(0<n≤4);(3)4
n(0<n≤4);(3)4![]() -4或4.
-4或4.
【解析】
(1)由△PCD,△EBC都是等腰直角三角形,得出CD=![]() PC,BC=
PC,BC=![]() CE,即可得出结论;
CE,即可得出结论;
(2)作PH⊥BD于H,首先利用四点共圆证明∠CBD=90°,再证明△CBD∽△CEP,求出BD、PH即可得出结果;
(3)分两种情形:①当BF=BD时,∠BDF=67.5°,在BC上取一点G,使得BG=BD,由BG+CG=BC构建方程即可得出结果;②当FB=FD时,∠FBD=∠FDB=45°,此时BD=BC=4![]() ,点E与点F重合,即可得出结果.
,点E与点F重合,即可得出结果.
(1)∵△PCD,△EBC都是等腰直角三角形,
∴CD=![]() PC,BC=
PC,BC=![]() CE,
CE,
∴![]() =
=![]() =
=![]() ,
,![]() =
=![]() =
=![]() ,
,
∴![]() =
=![]() ;
;
(2)如图1中,作PH⊥BD于H,
∵△PCD,△EBC都是等腰直角三角形,
∴∠PCD=∠BCE=45°,∠PBC=∠PDC=45°,
∴B、C、P、D四点共圆,
∴∠DBP=∠PCD=45°,
∴∠CBD=∠DBP+∠PBC=45°+45°=90°,△PBH是等腰直角三角形,
∵∠BCE=∠DCP=45°,
∴∠BCD=∠ECP,
∵∠CEP=∠CBD=90°,
∴△CBD∽△CEP,
∴![]() =
=![]() =
=![]() ,
,
∵PE=n,
∴BD=![]() n,
n,
∵tanA=![]() =
=![]() ,AC=6
,AC=6![]() ,
,
∴BC=4![]() ,
,
∴EC=BE=4,
∴PB=4+n,PH=BH=![]() (4+n),
(4+n),
∴S△BDP=![]() BDPH=
BDPH=![]() ×
×![]() n×
n×![]() (4+n)=2n2+
(4+n)=2n2+![]() n(0<n≤4);
n(0<n≤4);
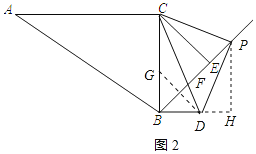
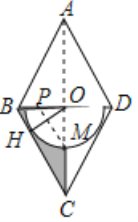
(3)①如图2中,当BF=BD时,在BC上取一点G,使得BG=BD,
∵∠PBD=45°,
∴∠BDF=67.5°,
∵∠CBD=90°,
∴∠BDG=∠BGD=45°,
∴∠BCD=∠GDC=22.5°,
∴GC=GD,
∵PE=n,BD=![]() n,
n,
∴BG=![]() n,CG=DG=
n,CG=DG=![]() BG=2n,
BG=2n,
∴BG+CG=BC=4![]() ,
,
∴![]() n+2n=4
n+2n=4![]() ,
,
∴n=4![]() -4,
-4,
∴PE=4![]() -4;
-4;
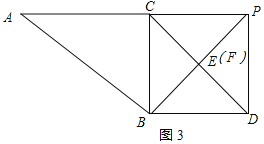
②如图3中,当FB=FD时,则∠FBD=∠FDB=45°,
此时BD=BC=4![]() ,
,
∵∠CDP=45°,
∴∠BDP=90°,
∵∠CPD=90°,∠CBD=90°,
∴四边形CBDP为正方形,E、F点重合,
∴PE=BE=4,
综上所述,线段PE的长度为:4![]() -4或4.
-4或4.