题目内容
【题目】如图，在四边形ABCD中，∠DAB=∠DCB=90°，CB=CD，AC=6，则四边形ABCD的面积是_________.
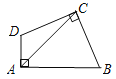
【答案】18．
【解析】
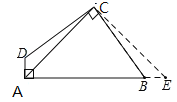
根据已知线段关系，将△ACD绕点C逆时针旋转90°，CD与CB重合，得到△CBE，证明A、B、E三点共线，则△ACE是等腰直角三角形，四边形面积转化为△ACE面积．
∵CD=CB，且∠DCB=90°，∴将△ACD绕点C逆时针旋转90°，CD与CB重合，得到△CBE，∴∠CBE=∠D，AC=EC，∠DCA=∠BCE．
根据四边形内角和360°，可得∠D+∠ABC=180°，∴∠CBE+∠ABC=180°，∴A、B、E三点共线，∴△ACE是等腰直角三角形，∴四边形ABCD面积=△ACE面积= 
AC2=18．
故答案为：18．
练习册系列答案
寒假大串联黄山书社系列答案
相关题目
